CS-137 Programming Principles

Notes by Daniel Prilik

Software Engineering Class of 2020

A note about these notes

They aren’t amazing, but they are pretty solid.
I may have missed a thing or two here and there, but i’ve tried not to miss any super important key concepts.
Also, brace yourself if you hate spelling errors. There are going to be quite a few (probably).

These note do not have any program flow diagrams, partly because I didn’t find them useful, but mostly because it would be a pain to actually write in markdown.

One last disclaimer: I give you no guarantees that these notes are accurate, so use them at your own risk.

That said, enjoy!

Office Hours

12:30 - 1:30 pm on Wednesdays

Table of Contents:

Lecture 1

Sept 14th 2015

Outline of the course

Basic C programming concepts
a) variables
b) integers, chars, expressions
c) conditionals
d) loops
Functions, parameters, arguments, and recursion
Arrays and Pointers
Structures
Sorting, searching, time and spave complexity // not covered in textbook
Other fun stuff :) // not covered in textbook

Core CS sequence

Term	Course	Name	Language
1A	CS 137	Programming Principles	(C)
1B	CS 138	Data Abstraction	(C++)
2A	CS 241	Sequential Programs	(MIPS, …)
2B	CS 247	Abstraction and Specification	(more C++)

Supplementary courses

Course	Name
SE 101	Foundations of Software Engineering
ECE 124	Arduino stuff
SE 212	Proving program correctness
ECE 222	How processors work
CS 240	Data Structures
CS 341	Algorithms

First C Program:

hello.c

    #include <stdio.h>

    int main(void) {
        printf("Hello World!\n");
        return 0;
    }

You can compile c programs on linux by running: gcc [-o (name of exe) ] (file *.c)

Lecture 2

Sept. 16th 2015

Using Euclid’s algorithm to find the Greatest Common Divisor (GCD)

First, we need two values:

x = 338 y = 806

$x = 338 \\ y = 806$

Now, we subtract one value from the other:

| x - y | = 468

$| x - y | = 468$

Somehow, we need to find a number that can evenly divide both x and x-y

That’s hard with big numbers, so instead, we make the problem smaller.

First, we set $y$ to be the abs difference of x and y:

y = | x - y | = 468

$y = | x - y | = 468$

Then, We simply repeat the algorithm on $x$ and $y$ again!

x = 338, y = 468 | x - y | = 130 = y

$x = 338, y = 468 \\ | x - y | = 130 = y\\$

And again…

x = 338, y = 130 | x - y | = 208 = y

$x = 338, y = 130 \\ | x - y | = 208 = y \\$

And repeat ad-nauseum until you get $| y-x | = 0$

In this case, the x and y values that subtract to 0 are 26, thus we know 26 is the GCD.

Using the MOD operator makes this process go faster, as it skips numbers.
sidenote: The mod operator returns the remainder between a quotient of 2 int’s

806 % 338 = 130 338 % 130 = 78 130 % 78 = 52 78 % 52 = 26 52 % 26 = 0

$806\ \%\ 338 = 130 \\ 338\ \%\ 130 = 78 \\ 130\ \%\ 78 = 52 \\ 78\ \%\ 52 = 26 \\ 52\ \%\ 26 = 0$

And, there we have it.
When using the MOD method, the GCD is the smaller number in the final MOD operation (in this case, 26).

This algorithm can be simply implemented in c as so:

gcd.c

    #include <stdio.h>

    int main(void) {
        int a = 806;    // Number 1
        int b = 338;    // Number 2
        int r = 0;      // Temporary storage var

        while (b!=0) {
            r = a % b;
            a = b;``
            b = r;
        }
        printf("%d\n", a);
        return 0;
    }

I proceeded to miss some notes about printf and scanf. Whoops.

Lecture 3

Sept 18th

Computer Memory

Computer memory is essentially a table of bytes

Index	Value of Byte
0	0010 0101
1	0110 1101
2	0100 1001
…

A single Byte (Binary Digit) is 8 Bits

Place Value	128	64	32	16	8	4	2	1
Digit Value	0	0	1	0	0	1	1	0

Typically, 4 bytes makes an int type

Sidenote: The number above would be 32 + 4 + 2 = 38₁₀

Index	Byte 1	Byte 2	Byte 3	Byte 4
0	0010 0100	0000 0010	0100 0010	0100 0101
1	0000 0010	0100 1000	0100 0100	1001 1001
2	1000 1000	0010 0101	0011 0010	0100 0100
…	0010 0010	1000 1000	1000 1000	0001 0001

This gives every index a total of 32 Bits with which to store info!

Variable types in C

Following are the typical sizes for variables in C:

Type	Bits	Bytes	Value Range
char	8	1	[-128, +127] i.e [-2⁷, +2⁷ - 1]
int	32	4	[-2³¹, +2³¹ - 1]
unsigned char	8	1	[0, +255]
short int	16	2	[-2¹⁵, 2¹⁵ - 1]
unsigned short int	16	2	[0, +2¹⁶ - 1]
unsigned int	32	4	[0, +2³² - 1]
long int	32 or 64	4 or 8
long long int	64	8	[-2⁶³, +2⁶³ - 1]
unsigned long long int	64	8	[0, +2⁶⁴ - 1]

Unsigned integers

An 8 bit number has the following memory layout:

Place Value	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Digit Value	b₇	b₆	b₅	b₄	b₃	b₂	b₁	b₀

The value of this byte in binary would be $b_7 \cdot 2^7 + b_6 \cdot 2^6 + ... + b_0 \cdot 2^0$

Examples:

0000 0000₂ = 0₁₀
0101 0101₂ = 1+4+16+64 = 85₁₀
1111 1111₂ = 1+2+4+8+16+32+64+128 = 255₁₀

Unsigned integers use all 8 bits of their memory to store a value, as opposed to Signed integers, that only use the last 7 bits of their memory to store a value.

Signed integers

Negative values are represented with two’s complement of their absolute value’s binary representation.

In two’s complement, the leftmost bit is the signing bit, and the remaining bits are used to store the value of the number.

If the signing bit is 0, the number is positive.
If the signing bit is 1, the number is negative.

But how do we actaully convert a negative number in Base 10 into a signed integer stored in Base 2? We follow these steps:

start with the unsigned binary
complement each bit
add 1

Example:
How do we represent -38₁₀ in binary?

First, we take it’s absolute value, and represent it in Binary:

3810 ⇓ 001001102

$38_{10} \\ \Downarrow\\ 0010\ 0110_2\\$

Then, we turn each 1 into a zero, and each 0 into a 1

00100110 ⇓ 11011001

$0010\ 0110\\ \Downarrow\\ 1101\ 1001$

We now have 1’s compliment, which is useless except to later get 2’s complement.

To get 2’s compliment, we add 1 to 1’s compliment:

110110012 + 1 = 110110102

$1101\ 1001_2 + 1 = 1101\ 1010_2$

Thus, we see that $-38_{10}$ can be expressed as $1101\ 1010_2$

Expressions in C

Let $a = 806$ and $b = 338$

Function	Operator	Example
add	+	a + b = 1144
subtract	-	a - b = 468
multiply	*	a * b = 272428
divide	/	a / b = 2 ( NOT 2.385 ) — Ints truncate
modulus	%	a % b = 130 ( remainder )

Order of Evaluation

C follows the basic elementary school rules of BEDMAS
C evaluates (in order): brackets, exponents, division, multiplication, adding, subtracting

so,that means that: a / b + a * b $\Longleftrightarrow$ (a / b) + (a * b)

Lecture 4

Sept 21st

Book-keeping

Quiz 0 will be on Friday, at the start of class. It will be about order of operations
Eg:

    a = 1;
    b = 2;
    c = 3;

    printf("%d\n", a - b * c);

Output: -5

Assignment 1 will be released tomorow, and will be due in a week.

Assignment

let $a = 806$ and $b = 338$
Take the following code sample:

    a = a + b; // 1144
    b = a / b; // 3
    b = b + 1  // 4

An interesting thing about the assinment operator: It has a return value!
c = a = a + b would set c to 1144, as a = a + b returns a + b!

Compund Assignment

We can rewrite a = a + 2 as a += 2
Similarly, for all other operations:

    a += 2;
    a -= 2;
    a *= 2;
    a /= 2;
    a %= 2;

Increment and Decrement

We can shorten a += 1 down even further by rewriting it as either:

++a pre-increment (evaluated before the rest of the expression)
a++ post-increment (evaluated after the rest of the expression)

Similarly, a -= 1 can be rewritten as either a-- or --a;

Example of how pre and post decrement matter:
let $a = 806, b = 338$

    a += ++b; // a = 1145, b = 339
    a += b++  // a = 1144, b = 2299
    a += --b  // a = 1143, b = 337
    a += b--  // a = 1144, b = 337

Operator Table

For a full table, refer to Table 4.2, on Page 63 of the Textbook
Appendix A has a complete table also.

Precedence	Operator	Associativity
1	++, - - (post)	left
2	++, - - (pre)	right
	+, - (unary*)	right
3	*, /, %	left
4	+, - (binary**)	left
5	=, +=, -=, *=, /=, %=	right

* Unary is when you do stuff like a = -a;
** Binary is when you do stuff like a = a + b

Examples:

Left associativity
- i - j - k $\Longleftrightarrow$ (i - j) - k
- i * j / k $\Longleftrightarrow$ (i * j) / k
Right associativity
- a = b = c $\Longleftrightarrow$ a = (b = c)
Combined example:
- 3 * b - ++c $\Longleftrightarrow$ (3 * b) - (++c)

Logical Expressions

C, being a stupid, old language, lacks dedicated boolean variables.
In C:
0 evaluates as False
Non-0 evaluates as True (Usually 1)

There are also:

Relational Operators: <, >, <=, >=
Equality Operators: ==, !=
Logical Operators: !, &&, ||
- || and && use short circuited evaluation, i.e: they always evaluate the left operand, and only evaluate the right operand if necesary.
  - for &&: if the left is false, the right is not evaluated
  - for ||: if the left is true, the right is not evaluated
- Examples:
```
  (100 > 700) || (2 >= 7)  // is True,  both ops were evaled
  (100 > 700) && (2 >= 7)  // is False, only the left op was evaled
  !(100 > 700) && (2 >= 7) // is False, both ops were evaled
```

The relational, equality, and logical operators return 1 if True, and 0 if False

`(i >= j) + (i == j)`	relation
0	`i > j`
1	`i < j`
2	`i == j`

These operators have their own precedence table:

operator	precedence	associativity
!	same as unary +,-	right
relational	lower than arithmetic	left
equality	lower than relational	left
logical	lower than equality	left

Example: i + j < k || ~k == 1 $\Longleftrightarrow$ ((i+j) < k) || ((!k) == 1)

Lecture 5

Sept. 22nd

Combined Operator Table

precedence	operator	associativity
1	++, — (post)	left
2	++, — (pre)	right
	+, - (unary)
	!, ~
3	*, /, %	left
4	+, - (binary)	left
5	<, <=, >, >=	left
6	=, !=	left
7	&	left
8	^	left
9	\|	left
10	&&	left
11	\| \|	left
12	? :	right
13	=, +=, -=, *=, /=, %=	right
	~=, &=, ^=, \|=

Bitwise operators

let $a = 2_{10}, b = 3_{10}$
thus $a = 0000\ 0101_{2}, b = 0000\ 0011_{2}$

The bitwise operators do the following:

Operator	Description	Example
~	NOT	`c = ~a` $\Longrightarrow c = 1111\ 1010$
&	AND	`c = a & b` $\Longrightarrow c = 0000\ 0001$
^	XOR	`c = a ^ b` $\Longrightarrow c = 0000\ 0110$
\|	OR	`c = a` \| `b` $\Longrightarrow c = 0000\ 0111$

DeMorgan’s Theourem

DeMorgan’s Theourem states that

! (P & & Q) = =! P | |! Q! (P | | Q) = =! P & &! Q

$!(P\ \&\&\ Q)\ ==\ !P\ ||\ !Q \\ !(P\ ||\ Q)\ ==\ !P\ \&\&\ !Q$

Proof:

P	Q	P && Q	!(P && Q)
0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	0

!P	!Q	!P \|\| !Q
1	1	1
1	0	1
0	1	1
0	0	0

Example of Application:
!( i >= 0 && i < n) $\Longleftrightarrow$ ~(i >= 0) || !(i < n) $\Longleftrightarrow$ i < 0 || i >= n

Selection Statements

In C, there are 2 types of selection statements:

if / else
switch

We’ll simply discuss if / else, read about switch yourself.

If statements come in two forms:

Single If

    if (expresson)
        statement

If / Else

    if (expresson)
        statement
    else
        statement

One can have nested ifs, but one must remember that if writing code without brackets, else will always match with the nearest unmatched if, regardless of indentation.
Example:

    int 0 = 3;
    if (i % 2 == 0)
        if (i == 0)
            printf("zero\n");
    else
        printf("how odd\n");

This code actually prints nothing! If you add brackets, you see why:

    int 0 = 3;
    if (i % 2 == 0) {
        if (i == 0) {
            printf("zero\n");
        } else {
            printf("how odd\n");
        }
    }

Another interesting thing to note: C doesn’t have an “else if” keyword!
How does C handle else if statements?
The following example explains:

    // Without Brackets vs With Brackets

    if (expr)           // if (expr) {
        // blah         //     // blah
    else if (expr)      // } else {
        // blah         //     if (expr) {
    else                //         //blah
        // blah         //     } else {
                        //         // blah
                        //     }
                        // }

Compound statements

Brace Brackets make one statement from 0, 1, 2, 3, … expressions
Example:

    if ( i == 0 )
        printf("zero\n");
    else {
        printf("even\n");
        printf("or\n");
        printf("odd\n");
    }

Conditional expression

C has this neat expresson: ? :
It is used in the following way. (condition) ? {if true} : {if false}
Essentially, it is a condensed if statement.

Example:

    if (i > j)
        printf("%d\n", i);
    else
        printf("%d\n", j);

Can be condensed into simply printf("%d\n", i > j ? i : j )

Boolean Values

C origionally did not have boolean values.
True was 1, False was 0.

In the C99 Specification, they added boolean values.

They are used as such:

    #include <stdbool.h>

    int main (void) {
        bool first = true;

        for (;;) {
            if (true)
                first = false;
            else
                printf("Boop")
        }
        return 0;
    }

Lecture 6

Sept 25th

While Loop

While loops execute 0 or more times
Example of a While loop:

    int r = a % b;
    while (r != 0) {
        a = b;
        b = r;
        r = a % b;
    }

Do While Loop

Do While loops execute 1 or more times
Example of a Do While loop:

    do {
        r = a % b;
        a = b;
        b = r;
    } while (r != 0);

Functions

We can rewrite GCD as a function:

    int gcd (int a, int b){
        int r = a % b;
        while (r != 0) {
            a = b;
            b = r;
            r = a % b;
        }
        return b;
    }

If we define this function in a program, we can then write something like this:

    #include <stdio.h>

    int gcd (int a, int b){
        int r = a % b;
        while (r != 0) {
            a = b;
            b = r;
            r = a % b;
        }
        return b;
    }

    int main (void) {
        printf("%d\n", gcd(806, 338));  // prints out 26
        printf("%d\n", gcd(15, 27));    // prints out 3
        return 0;
    }

int before gcd is the return type of the function
int a and int b are called the parameters of the function
806 and 338 are called the arguments passed to the function
This entire code block is called a function definition

NOTE: To use a function, you MUST declare it before it is invoked!

Lecture 7

Sept 28th

Nothing important hopefully…

Lecture 8

Sept 29th

Assertions

Assertions can be inplemented by including the assert.h header library, and by calling assert(exp) somewhere in a program.

If expr evaluates to true, nothing happens.
If expr evaluates to false, it terminates the program with a message stating:

the filename
line number
function name and expression

Evidently, assert is supremely useful for debugging.

Here is an example relevant to A2_02

    #include <assert.h>
    ...
    bool leap(int year) {
        assert(year >= 1753);
        if (year % 400 == 0) {
        ...etc
    }

Asserts can be left in a program even when pushing code in production, and in fact, they should!

Programmers make assumptions when programming and then forget about them
Assertions cause a program to fail “loudly” when these assumptions are broken, rather than failing “softly” (continuing to execute regardless of error)
Asserts protect against future modifications that insert logic errors into the program

Seperate Compilation

What if we want to compile a program from multiple files?

Say we have 2 c files that depend on one another:

powers.c

    /* Defines the functions */
    int square(int num) { return num * num; }
    int cube(int num) { return square(num) * num; }
    int quartic(int num) { return square(num) * square(num); }
    int quintic(int num) { return cube(num) * square(num); }

Notice the lack of main!

main.c

    #include <stdio.h>

    /* Below we declare:
         1) That these functions exist
         2) The return type of these functions
         3) The parameter types of the functions
    */
    int quartic(int num); // does not have to have the same
    int quintic(int num); // parameter name as in powers.c

    void testQuartic (int num) { printf("%d^4 = %d\n", num, quartic(num)); }
    void testQuintic (int num) { printf("%d^5 = %d\n", num, quintic(num)); }

    int main() {
        testQuartic(3);
        testQuintic(2);
    }

To compile the two source files together, we have to run a modified gcc command:
gcc -o powers main.c powers.c (order of source files should not matter)

Header Files

Header files declare functions (and a whole bunch of other stuff that we don’t care about right now.)

For example, the powers program above could be rewritten to use a header file

powers.h

    #ifndef POWERS_H  // For if we accidentally include a duplicate header file
        #define POWERS_H
        int square(int num);
        int cube(int num);
        int quartic(int num);
        int quintic(int num);
    #endif

powers.c

    *** Stays the same ***

main.c

    #include <stdio.h>
    #include "powers.h"

    ... stays the same ...

Using a header does not change the compiler arguments, so to compile the two source files together, we still just run: gcc -o powers main.c powers.c

Lecture 9

Oct 2nd

Recursion

Recursion is having a function call itself.

For example, let’s rewrite gcd.c recursively:

gcdr.c

    int gcd(int a, int b) {
        if (b == 0) return a;
        return gcd(b, a % b);
    }

Dayum. Ain’t that short!

Pass by Value

Take the following code:

    void weird (int n) {
        n = 17;
    }

    void main () {
        int n = 6;
        weird(n);
        printf("%d\n", n);
    }

What do you think it outputs?
It’s not 17! It’s actually 6!

This is because all that weird did was make a locally scoped variable and set it’s value. Just because the two variables had the same name, does not mean that one changes the value of the other!

Arrays

This is a scalar: int a = 6;
6 is the initalializer for the array.

In memory, it looks like this:

var	val
a	6

This is an array: int a[5] = {10, -7, 3, 8, 42};
10, -7, 3, 8, 42 are all initializers for a.

In memory, it looks like this:

var	val
a	10
	-7
	3
	8
	42

Size can be set either:
explicitly: int a[5] = {10, -7, 3, 8, 42};
implicitly: int a[] = {10, -7, 3, 8, 42};

When defining implicitly, C sets the size of the array to the number of elements it was initialized with.

If defining explicitly, but only defining a few of the values, C fills the rest of the array with 0’s
Eg: int b[5] = {1,2,3} == {1,2,3,0,0};
Eg: int c[5] = {0} == {0,0,0,0,0};

If you don’t initialize an array with values, it will still be allocated in memory, but referencing the array will yield garbage…
Eg: int d[5]; == {?,?,?,?,?}

Arrays are 0 indexed.
When referencing an element of an array, C counts the first element as element 0
Eg: a[3] = {1,2,3}; printf("%d\n", a[2]); outputs 3

Lecture 10

Oct 6th

Sieve of Eratosthenes

The Sieve of Eratosthenes finds all primes up to a number n (some upper bound)

Eg: Given n=20, the function returns 2,3,5,7,11,13,17,19

The alogorithm works by starting with 2, marking it as prime, and then crossing out all multiples of 2. Once it gets to the upper bound, it goes on to the next non-corssed out number (3), and crosses out all of it’s multiples. It continues to do this until it hits a number $\leq \sqrt{n}$

An implementation in C follows:

sieve.c

    #include <stdio.h>
    void sieve(int a[], int n) {
        // a[] is variable sized, so we must also
        // pass n, the size of the array

        if (n <= 0) return; // empty array
        a[0] = 0;
        if (n == 1) return; // just 1
        a[1] = 0;
        if (n == 2) return; // just 1 and 2

        // set the rest of the numbers to 1
        // as they may be prime
        for (int i = 2; i < n; i++) a[i] = 1;

        for (int i = 2; i <= (n-1)/i; i++) {
            if (a[i]) {
                for (int j = 2*i; j < n; j += i) {
                    a[j] = 0;
                }
            }
        }
    }

    void main () {
        int n;
        scanf("%d", &n);
        int a[n+1];
        sieve(a, n+1);

        for (int i = 0; i <= n; i++) {
            if (a[i]) printf("%d\n", i);
        }
    }

Sizeof Operator

sizeof(type) Returns the size of the type in bytes
sizeof(var) Returns the size of the variable in bytes
It is usually implemented at runtime (so variable length arrays don’t play nicely with it)

Take the following example:

    void strange(int a[], int n) {     // a is JUST A POINTER!
        printf("%d\n", sizeof(a));     // Either 8 (or 4)
                                       // Depends of size of pointer implement
    }
    void main() {
        int i;
        int a[10] = {0};

        printf("%d\n", sizeof(int));   // 4
        printf("%d\n", sizeof(i));     // 4
        printf("%d\n", sizeof(char));  // 1
        printf("%d\n", sizeof(a));     // 40 ---- this is a known size arr

        int n = sizeof(a)/sizeof(a[0]); // gives length of arr, 
                                        // even if variable length
        stange(a, n);

        int m; scanf("%d", &n); // INPUT 8
        int b[n];
        printf("%d\n", sizeof(b)); //32
    }

Lecture 11

Oct 7th

Array Pointers

Look at this code:

    int a[5] = {0,1,2,3,4};
    printf("%lu\n", (unsigned long)a); // Prints "140737326347974"

What the hell is that thing?!

It’s a pointer to the first item in the array in memory!

Because a is just a pointer, we can rewrite functions that take arrays using pointer notation, i.e:
void foo (int a[], int n) can be rewritten as void food (int *a, int n)

Keep in mind that even though you can use pointer notations, you probably shouldn’t, as pointer notation usually obfuscates the nature of the function for those who have to look at it.

Weird things happen when assigning arrays to other variables:

    void main () {
        int a[] = {0,1,2,3,4};
        int *b = a;

        printf("%d\n", a[2]);  // prints 2
        b[2] = 100;
        printf("%d\n", a[2]);  // prints 100
    }

a and b point to the same memory adress, so any edits to one affect the other.

Multidimensional arrays

Arrays within Arrays within Arrays, Oh my!

    int a[4][3] = {
        {11,12,13},
        {21,22,23},
        {31,32,33},
        {41,42,43}
     };

     printf("%d\n", a[1][2]); // 23

    int sum = 0;
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 3; j++) {
            sum += a[i][j];
        }
    }

     printf("%d\n", sum);

A little caveats of multidimensional arrays:
When defining a function that takes a multidemensional array, one must specify all but the first dimension!
eg: int sum(int a[][3][4], int n) is valid
eg: int sum(int a[][][4], int n, int m) is NOT valid

Floating Point Numbers

C stores floating points using Scientific Notation (eg: $-2.6302 * 10^{30}$ )
The memory used in such a number is divided between the precision of the number (-2.6302), and the range of the number (30).

There are a few different types of floating point numbers:

type	storage	precision	range
float	4 bytes	~7 digits	+- 38
double	8 bytes	~16 digits	+-308
long double	16 bytes	~31 digits	+-4931

Look at the following code for an example of how to use floats:

    float z = 1.0f    // use float as type, and f to cast number as float
    double y = 1.0;   // not always neccessary to cast number when assigning

    void main () {
        double x = -2.6302e30; // yet another way to define floats

        printf("%d\n", sizeof(x)) // 8 [bytes];
        printf("%f\n", x)' // -26302 000 000 000 00 123 564 578 345 000 000

        // there is gibberish in the number due to
        // binary being unable to perfectly represent
        // some decimal numbers

        printf("%.2e\n", x); // -2.63e+30
        // The .2 truncates the float, and e prints it in scientific notation

        printf("%g\n", x); // -2.6302e+30
        // %g prints out whatever is shorter between %e and %f (int this case %g)
    }

Lecture 12

Oct 7th (Again)

The IEEE 754 Floating Point Standard

Double Precision numbers are 64 bits, with the following layout:

Bit 63: Sign (1 is negative, 0 is positive)
Bits 62-52: Exponent
Bits 51-0: Fraction

Eg: +1.1e2^1 = 0|100 000 000 000|10000...

Floating points are only approximations of real numbers.
Eg: $0.1_{10}$ cannot be represented perfectly in binary. It’s binary representation is $0.0001111..._{2}$

Representaion Error

Let r be a real number
Let p be the approcimated value

The absolute error is $| p - r |$
eg: $|3.14 - \pi| \approx 0.0015927$

The relative error is $\frac{|p-r|}{|r|}$
eg: $\frac{|3.14-\pi|}{|\pi|} \approx 0.000507$

Relative error can be very large if r is small.
Thus, care is required when:

a) subtracting nearly equal numbers
b) dividing by very small numbers
c) multiplying by very large numbers
d) tests for equality

Example of riskyness:

    double x = 5.0/6.0;
    double y = 1.0/2.0;
    double z = 1.0/3.0;

    if (x-y == z) printf("equal\n");
    else printf("not equal\n");

    // Prints 'not equal'

Smarter to rewrite it as:

    #define EPSILON 0.00001

    // can use fabs() instead of || below
    if (x - y - z < EPSILON || x-y-z > -EPSILON) printf("equal\n");
    else printf("not equal\n");

    // Prints 'equal'

Lecture 13

Oct. 9th

Polynomials

You can represent polynomials as an array of coefficients.
Ex: $f(x) = 3x^3 +4x^2+6$ can be represented as double f[] = {3,4,0,6}

Evaluating the polynomial is also pretty easy:

poly.c

    #include <stdio.h>
    #include <assert.h>

    double eval_p(double f[], int n, double x) {
        assert(n > 0);

        double y = f[0];
        double p = 1.0;

        for (int i = 0; i < n; i++) {
            p *= x;
            y += f[i]*p;
        }

        return y;
    }

    int main () {
        double f[] = {2,9,4,3};
        printf("%f\n", eval_p(f, 4, 2));

        return 0;
    }

This is the intuitive implementation.
There are:

2(n-1) float multplies
n-1 float additions

Not bad… but there is a more efficient method!
It is called Horner’s Method

Horner’s Method

A polynomial such as

f (x) = 3 x 3 + 4 x 2 + 9 x + 2

$f(x) = 3x^3+4x^2+9x+2$

Can be rewritten as

f (x) = 2 + x (9 + x (4 + 3 x))

$f(x) = 2+x(9+x(4+3x))$

We can leverage this fact to make a more efficient algorithm:

poly_h.c

    #include <stdio.h>
    #include <assert.h>

    double horner(double f[], int n, double x) {
        assert(n > 0);

        double y = f[n-1];

        for (int i = n - 2; i >= 0; i--) {
            y = x*y + f[i];
        }

        return y;
    }

    int main () {
        double f[] = {2,9,4,3};
        printf("%f\n", horner(f, 4, 2));

        return 0;
    }

This implementation only has:

n-1 float multplies
n-1 float additions

Dat efficiency doe.

Math.h Highlights

    #include <math.h>

    // Trig
    double sin  (double x); // sine
           cos            // cosine
           tan            // tangent
           asin           // sin-1
           acos           // cos-1
           ...            // etc

    // Exponents
    double exp   (double x);           // e^x
           log                      // ln x
           log10                    // log x 
           sqrt                     // squrt
           pow   (double x, double y)  // x^y

    // Misc.
    double ceil  (double x);
           floor
           fabs

    // Constants
        M_PI      // pi
        M_PI_2    // pi/2
        M_E       // e
        M_LN2     // ln(2)
        M_SQRT2   // sqrt(2)
        NAN       // not-a-number
        INFINITY  // Guess.

Lecture 14

Oct 14th

The Bisection Algorithm

We can approximate the roots of a function using the Bisection Algorithm.

Refer to MATH 117 Notes for details on the algorithm.

As a refresher, the algorithm is as follows:

1) Start with some $a$ and $b$ where $f(a) < 0$ and $f(b) > 0$
2) Compute the midpoint $m = (a+b)/2$
3) if $f(m) < 0$ then $a = m$ , else $b = m$
4) GOTO 2 as many times as one likes for precision

Note: This algorithm only works accurately when there is only one root between a and b.

Obviously, we can rewrite this algorithm in C:
This program caluclates the root of the function $f(x) = x - cos(x)$

bisect.c

    #include <assert.h>
    #include <math.h>
    #include <stdio.h>

    double f(double x) {
        return x-cos(x);
    }

    double bisect(double a, double b, double epsilon, int max_iter) {
        assert(f(a) * f(b) < 0 && epsilon > 0);
        double m, fm;
        for (int i = 0; i < max_iter; i++) {
            m = (a+b)/2;
            fm = f(m);
            if (fabs(fm) <= epsilon) return m;


            if (f(a)*fm < 0)
                b = m; 
            else 
                a = m;
        }
        return m;
    }

    int main(void) {
        printf("%g\n", bisect(-10, +10, 0.001, 100000));
        return 0;
    }

How can we calculate the number of iterations it took to calculate x?

we start with $\frac{b-a}{2}$
each iteration reduces the distance by half
Thus, using math…
$ϵ = b - a 2 \cdot 1 2 \cdot 1 2 \cdot 1 2 . . . (x t i m e s) ϵ = b - a 2 \cdot 2 - x 2 x = b - a 2 ϵ l o g (2 x) = l o g (b - a 2 ϵ) x = l o g ( b - a 2 ϵ ) l o g ( 2 )$ $\epsilon = \frac{b-a}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} ... (x\ times) \\ \epsilon = \frac{b-a}{2} \cdot 2^{-x} \\ 2^x = \frac{b-a}{2\epsilon} \\ log(2^x) = log(\frac{b-a}{2\epsilon}) \\ x = \frac{log(\frac{b-a}{2\epsilon})}{log(2)}$

In our example above, $x \approx 13$

Fixed-Point Iteration

FPI is yet another root finding method

Given $f(x) = x - cos(x)$ , we want $x_0$ such that $f(x_0) = 0$

x - c o s (x) = 0 g (x) = c o s (x)

$x - cos(x) = 0 \\ g(x) = cos(x)$

We start with a rough guess…

x n + 1 = g (x n)

$x_{n+1} = g(x_n)$

And we repeat until $|x_{n+1} - x{n}|< \epsilon$

Note: THIS DOES NOT ALWAYS CONVERGE.

In C, this function is written as:

fixed.c

    #include <assert.h>
    #include <math.h>
    #include <stdio.h>

    double g(double x) {
        return cos(x);
    }

    double fixed(double guess, double epsilon, int max_iters) {
        for (int i = 0; i < max_iters; i++) {
            double gx = g(guess);
            if (fabs(gx-guess) < epsilon) return gx;
            guess = gx;
        }
        return guess;
    }

    int main(void) {
        printf("%g\n", fixed(0, 0.001, 100000));
        return 0;
    }

Function Pointers

Functions can be passed as arguments to other functions!

So, if we want to pass a function like double f(double x) as a parameter, we would use the form double (*f)(double)

Eg:

    double f(double x) { return x; }
    double eval_func(double x, double (*h)(double)) { return h(x); }

We can use this property to generalize bisect() to work with any function:

    double f0(double x) { return x*x-3; }
    double f1(double x) { return cos(x) - x; }

    void main () {
        printf("%g\n", bisect(-10, +10, 0.001, 100000, f0));
        printf("%g\n", bisect(-10, +10, 0.001, 100000, f1));
    }

Topics covered on the midterm

Basics: Variables, Expressions, Loops, Conditionals
Ints, Doubles
Functions (function pointers)
Arrays
Math.h
Algorithms: Euclid’s, Horner’s, Bisection

Lecture 15

Oct 16th

Structures

Structures (structs) are compound data types.
They group several named member variables together in memory, so that they can all be accessed using just one name (pointer).

A simple example would be a struct that holds the time of day (in 24h time):

    struct tod {
        int hours;
        int minutes;
    };

Here is how one would actually use that struct in a program:

    void main() {
        struct tod now = {16,50}; // or {.hours = 16, .minutes = 50};
        struct tod later;

        later.hours = 18;
        later.minutes = 0;

        printf("%d:%d\n", now.hours, now.minutes);        // 16:50
        printf("%d:%02d\n", later.hours, later.minutes);  // 18:00
    }

We can also use structs as parameters:

    void todPrint(struct tod when) {
        printf("%02d:%02d\n", when.hours, when.minutes);
    }

    void main() {
        struct tod later {18,0};
        todPrint(later);
    }

Can we return structs? Hell yeah we can!

    struct tod todAddTime(struct tod when, int hours, int minutes) {
        when.minutes += minutes;
        when.hours += hours + when.minutes / 60;

        when.minutes %= 60;
        when.hours %= 24;

        return when;
    }

    void main() {
        struct tod now = {16, 50};
        now = todAddTime(now, 1, 10);
        todPrint(now);
    }

We can simplify declaring structs using typedefs:

    typedef struct {
        int hours;
        int minutes;
    } tod;

    void main() {
        tod now = {16, 50};
        ...
    }

Designated Initializers

Sidenote: When defining a structure, you can specify fields to initialize by name, and any unnamed fields are set to 0.

eg: tod later = {.minutes = 60} makes tod={0,60}
eg: int a[6] = {[4]=1, [1]=2} makes {0,2,0,0,1,0}

Lecture 16

Oct 26th

Complex Numbers

Before programming with complex numbers, we must first understand what complex numbers actually are.
Complex Numbers are numbers that have the following format:

x + y i

$x + yi$

Where $i=\sqrt{-1}$ or $i^2 = -1$ .

As youcan see, complex numbers consist of two components:

$x$ is the real component.
$yi$ is the imaginary component

Here are the various operations we can do with complex numbers:

Addition: $(x+yi) + (w + zi) = (x + w) + (y+z)i$
Multiplication: $(x+yi)(w + zi) = (xw - yz) + (xz + yw)i$

Complex Numbers in C89

While C99 added a complex numbers library, C89 does not have one, so programmers had to write their own implementation.
Let’s write our own implementation. Why? Because.

cplex.h

    #ifndef CPLEX.H
    #define CPLEX.H

        // Define the Complex Number struct
        typedef struct {
            double r;
            double i;
        } cplex;

        // Declare functions to work with cplex structs
        cplex cplexConstruct(double r, double i);
        cplex cplexAdd(cplex a, cplex b);
        cplex cplexMult(cplex a, cplex b);
        void cplexPrint(cplex a);

    #endif

cplex.c

    #include <stdio.h>

    #include "cplex.h"

    cplex cplexConstruct(double r, double i) {
        return (cplex) {.r = r, .i = i};
    }
    void cplexPrint (cplex a) {
        printf("%g + %gi\n", a.r, a.i);
    }

    cplex cplexAdd(cplex a, cplex b) {
        return (cplex) {
            .r = a.r + b.r,
            .i = a.i + b.i
        };
    }
    cplex cplexMult(cplex a, cplex b) {
        return (cplex) {
            .r = a.r * b.r - a.i * b.i,
            .i = a.r * b.i + a.i * b.r
        };
    }

cplexMain.c

    #include "cplex.h"

    int main () {
        cplex a = cplexConstruct(1,2);
        cplex b = cplexConstruct(3,4);

        cplex c = cplexAdd(a,b);

        cplexPrint(c);

        c = cplexMult(a,b);

        cplexPrint(c);

        return 0;
    }

Ah, another important note:
if (a == b) is NOT a valid way to check equality between two structs!

Complex Numbers in C99+

TL;DR: It’s better.

cplexMain.c

    #include <complex.h>
    #include <stdio.h>

    void main () {
        double complex a = 1 + 2*I;
        double complex b = 3 + 4*I;

        double complex c = a + b;

        printf("%g + %gi\n", creal(c), cimag(c));

        c = a * b;

        printf("%g + %gi\n", creal(c), cimag(c));

        return 0;
    }

Lecture 17

Oct 28th

Pagerank

How does Google figure out what you’re looking for?
Well, they use a variety of variables:

content of webpages (anchor text mainly)
user behavior
webpage rank (which is static)

That last one is what we want to focus on.

Pagerank is a static list of webpages.
It is sorted by how “good” the website is.

The rank of a website, i.e: how “good” it is, is determined by how many other websites link to the webpage (logic being that a good website would be reffered to my many other websites).

How does Google build this Pagerank listing?

They might use the Random Surfer Model.
This is how it works:

pretend you are surfing randomly
at each step, you either:
- follow a link (probability $\delta$ ) OR
- Jump to a random page (probability $1-\delta$ )
The Pagerank of a page Q, R(Q), is the probability that you are on page Q after surfing for a long time.

R(Q) is calculated accoring to the following formula:

R (Q) = 1 - δ N + δ \sum P \to Q R ( P ) o u t ( P )

$R(Q) = \frac{1-\delta}{N} + \delta\sum\limits_{P \rightarrow Q} \frac{R(P)}{out(P)}$

Where:

$N$ is the Total Number of Pages.
$\sum\limits_{P \rightarrow Q}$ is the sum of all pages pointing to Q
$R(P)$ Pagerank of page linking to Q
$out(P)$ Pagerank of page linked from Q

Let’s take an example of a simple web:

X links to Y and Z, and is linked to by Y
Y links to X, and is linked to by Y and Z
Z links to Y, and is linked to by X

$R(X) = \frac{1-\delta}{N} + \delta \frac{R(Y)}{1}\\ R(Y) = \frac{1-\delta}{N} + \delta (\frac{R(X)}{2} + R(Z))\\ R(Z) = \frac{1-\delta}{N} + \delta \frac{R(X)}{2}$

If $\delta = 80\% = \frac{4}{5}$ Thus $\frac{1-\delta}{N} = \frac{1}{15}$

We can then solve a system of linear equations to find X, Y, and Z.
But I’m not going to solve those by hand, no, that would be too easy…

Let’s use our old friend fixed-point iteration!

Let our initial guess be that $x = y = z = 0.333...$
- new $x = \frac{1}{15} + \frac{4}{5}(y=0.333...)$
- new $y = \frac{1}{15} + \frac{2}{5}(x=0.333...) + \frac{4}{5}(z=0.333...)$
- new $z = \frac{1}{15} + \frac{2}{5}(x=0.333...)$
Repeat ad-nauseum intill we get a good answer.

After 20 iterations: $x = 0.383, y = 0.396, z = 0.220$

For the whole web, this would take thousands of iterations.

Sidenote: FPI doesn’t always converege, but it usually does, so that’s good.

Lecture 18

Oct 30th

Caveats of FPI in computing pagerank

Take an example of the following web:

X link to Y and Z
Y links to Z, and is linked to by X
Z is linked to by X and Y

Note that Z is a sink, i.e: it does not link to any pages at all

Writing out the equations for pagerank results in the following:

$\delta = \frac{4}{5}\\ R(X) = \frac{1-\delta}{N} = \frac{1}{15}\\ R(Y) = \frac{1-\delta}{N} + \delta \frac{R(X)}{out(X)} = \frac{1}{15}+\frac{4}{5}\frac{R(X)}{2}\\ R(Z) = \frac{1-\delta}{N} + \delta \frac{R(X)}{out(X)} + \delta \frac{R(Y)}{out(Y)} = \frac{1}{15}+\frac{4}{5}\frac{R(X)}{2} + \frac{4R(Y)}{5}\\$

This is problematic as it “removes” probability from the web.

Representing the Web as an Arary of Structs

Let’s define the web as used in Lecture 17 Part 1 in C.

First, we define a struct for each link:

    typedef struct {
        int src, dst;
    } link;

Now, we can make an Array of Links to represent the web:

    link l[] = {
        {0,1}, {0,2},   // page X
        {1,0},          // page Y
        {2,1}           // page Z
    }

Lets write a program to solve the system of equations!

pagerank.c

    #include <stdio.h>

    typedef struct {
        int src, dst;
    } link;

    // it may not be super efficient with loops
    // but it's readable and comprehensible
    void pagerank (link l[], int n_link, double r[], int n_page, double delta, int n_iter){
        double s[n_page];   // holds a temp copy of the new ranks
        int out[n_page];    // out(P)

        for (int i = 0; i < n_page; i++) out[i] = 0;
        for (int j = 0; j < n_link; j++) out[l[j].src]++;

        // initial guess
        for (int i = 0; i < n_page; i++) r[i] = 1.0 / n_page;

        // fixed-point iteration implementation
        for (int k = 0; k < n_iter; k++) {
            for (int i = 0; i < n_page; i++) s[i] = (1.0 - delta) / n_page;
            for (int j = 0; j < n_link; j++) 
                s[l[j].dst] += (r[l[j].src]/out[l[j].src])*delta;

            //copy s to r
            for (int i = 0; i < n_page; i++) r[i] = s[i]; 
        }
    }

    void main () {
        link l[] = {{0,1},{0,2},{1,0},{2,1}};
        double r[3];
        pagerank(l, sizeof(l)/sizeof(l[0]), r, 3, 0.80, 20);
        for (int i = 0; i < 3; i++) printf("%g\n", r[i]);
    }

Do note that for the real WWW, n_iter is probably going to be in the 100’s to 1000’s.

Lecture 19

November 2nd

Pointers

What the hell is a pointer?

Well, it’s a variable that “points” to location in memory that has a certain data type.
But that’s technical mumbo jumbo, what does it actually mean?

When we write int i = 6;, we tell C to allocate a 8 bit chunk of memory to store the value of 6, and to label that location in memory with the variable i.
So, when we then write i = 4, C knows what memory location i reffers to, and changes the value in that memory block to 4.

Now, what if we write int *p;
The hell is that asterisk doing there?
Well, this asterisk specifies that the variable being declared is a special type of variable, a pointer
The variable p does not itself contain an integer, but instead, it contains the location of a memory adress where an integer resides.
Initially, p does not point to any specific location, and accesing it without setting a pointee is very dangerous.

Say we want to tell *p to point to i‘s location in memory.
We write p = &i, where & references i, that is, it returns not the value at I, but i‘s actual memory adress.

Now that p points to the memory location of i, we can use *p = 10 to chnge the value of i to 10! That * derefrences the memory location that p contains.

That’s the gist of it, let’s see an example:

    int i = 6;
    int *p;

    p = &i;
    *p = 10;

    printf("%d \n", i);  // 10

    int *q;
    q = p;
    *q = 17;

    printf("%d \n", i);  // 17

Notice that multiple pointers can point to the same adress in memory!

Alright, that’s neat and all, but why are pointers useful?

Well, if you pass pointers to a function, that function is able to modify variables outside of it’s scope!

Take the following example:

swap.c

    #include <stdio.h>

    void swap(int *p, int *q) {  // takes memory locations and derefs them
        int temp = *p;
        *p = *q;
        *q = temp;
    }

    void main () {
        int i = 0; j = 2;
        swap(&i, &j);            // passing the memory locaiton of i and j
        printf("%d %d\n", i, j);
    }

SIDENOTE: There is a one line version of swap put forth by our resident genius:
if (x!=y) *x = *x ^ *y ^ (*y = *x);
How does this work? Good question. XOR’s apparently. I dunno, I just wrote it down.

Alright, what else can pointers be used for?
Well, we can have functions that return pointers.
Here is an example:

largest.c

    #include <stdio.h>

    int *largest(int a[], int n) {
        int m = 0;
        for (int i = 1; i < n; i++) {
            if (a[i]>a[m]) m = i;
        }
        return a + m;   // or return &(a[m]);
    }

    void main () {
        int test[] = {0,1,2,3,4,3,2,1,0};
        int *p = largest(test, sizeof(test)/sizeof(test[0]));
        printf("%d\n", test[*p]);
    }

You might be wondering, what the hell is return a + m? Well, it’s an example of…

Pointer arithmentic

There are a few different arithmetic operations we can preform on pointers:

We can add an int to a pointer
We can subtract and int from a pointer
We can subtract pointers from one another (so long as they are the same type)

Example:

    int a[8] = {2,3,4,5,6,7,8,9};
    int *p, *p, *q, i;

    p = &(a[2]); // p points to a[2]
    q = p + 3;   // q points to a[5]
    p += 3;      // p points to a[5]
    p = q - 3    // p points to a[2]
    i = q - p;   // i = 3
    i = p - q;   // i = -3

We can also compare pointers using all the usual relational operators > < ==, etc.

Here is an example that heavily employs pointer arithmetic:

sumarray.c

    int sum (int a[], int n) {
        int total = 0;
        for (int i = 0; i < n; i ++)  // OR: for (int *p = a; p < a + n; p++)
            total += *(a + i);        //         total += *p; 
        return total;
    }

Neat.

Now, here’s something to challenge your brain a bit…

ksplice pointer challenge

What does this code print out?
(assuming x points to memadress 100, and an int is length 4)

    $include <stdio.h>
    void main() {
        int x[5];
        printf("%p\n" x);       // 100
        printf("%p\n" x + 1);   // 104
        printf("%p\n" &x);      // 100 (because apparently x == &x)
        printf("%p\n" &x + 1);  // 120 (because int (*x)[5] + 1)
    }

Lecture 20

Nov 4th

Characters

C stores characters in char variables, 1 byte signed integers.
C uses the ASCII system for converting between these integers and characters.

ASCII is:

A 7-bit code for repeating characters
0000000-1111111 Means that an ASCII char has 128 possible values
ASCII is divided into a few char “groups”
- 00 - 31: Control Characters
- 48 - 57: digits ‘0’ to ‘9’
- 65 - 90: letters ‘A’ to ‘Z’
- 97 - 122: letters ‘a’ - ‘z’

NOTE: A full ASCII table is available in a multitude of places online

In C, we can represent characters as their integer counterparts by enclosing the char in single appostrophes.

Here is a sample piece of code to show off some properties of chars:

    char c = 'a'     // 97
    c = 65           // 'A'
    c += 2           // 'C'
    c += 32          // 'c'
    c = '\n'         // newline char
    c = '\0'         // null character

Now, ASCII worked fine when all computers had to represent was English, but as time went on, and the world became globalized,the world needed a system that would support all the characters out there from all languages, so that anyone could communicate with everyone. That’s why we now have…

Unicode

Unicode assigns “codepoints” to over 100000 characters from many languages (both living and dead, even pretend!).
A unicode character spans 21 bits, and has a range [0, 2²¹ - 1], or 3 bytes per character.

Eg: The mandarin character ‘sun’ has the unicode 26085₁₀ or U+65E5 in Hex

An awesome thing about Unicode is that it shares data values with ASCII!
Unicode ‘a’ is 97₁₀ = U+0061 = 110 0001₂, which is the same as ASCII

The unicode spec jsut defines the codes for each characters, there are still different ways to actually encode unicode.
Popular specs include: UTF-8, UTF-16, UTF-32, UCS-2

But by far the most popular and best supported one is UTF-8

UTF-8 - Unicode Transformation Format

UTF-8 is a Variable Length unicode representation, and is also backwards compatible with traditional ASCII

1-byte characters, i.e: codepoints 0-127, are ASCII chars
2-byte characters are up to 11 bits long, with a range [128, 2¹¹ - 1 (i.e 2047)]
3-byte characters are up to 16 bits long, with a range [2048, 2¹⁶ - 1 (i.e 65535)]
4-byte characters are up to 21 bits long, with a range [65536, 2²¹ - 1 (i.e: 2097151)]

Bits Codepoint UTF-8

1 XXX XXXX 0XXX XXX

2 XXXXX YYYYYY 110XXXXX 10YYYYYY

3 XXXX YYYYYY ZZZZZZ 1110XXX 10YYYYYY 10XXXXXX

4 XXX YYYYYY ZZZZZZ WWWWWW 11110XXX 10YYYYYY 10ZZZZZZ 10WWWWWW

Bits	Codepoint	UTF-8
1	`XXX XXXX`	`0XXX XXX`
2	`XXXXX YYYYYY`	`110XXXXX 10YYYYYY`
3	`XXXX YYYYYY ZZZZZZ`	`1110XXX 10YYYYYY 10XXXXXX`
4	`XXX YYYYYY ZZZZZZ WWWWWW`	`11110XXX 10YYYYYY 10ZZZZZZ 10WWWWWW`

Eg. That ‘sun’ character from before with code 26085₁₀ has the 3 bit UTF-8 encoding
1110 0110 10 010111 10 100101

Unicode in C

Starting with C99, C has a standard library for working with Unicode.
#include <wchar.h> is what you have to use.
You can read up about it on the internet, / on textbook page 650

NOTE: In this course, we will be using ASCII for everything. Unicode is just good to know!

Now, for something completely different:

More about Pointers

Pointers can be Null pointers, or a pointer to nothing.
We can make a null pointer by casting 0 to a pointer like so: (void*)0
So, to make a int* null pointer, we do int *p = (int*)0;
It works similarly, for doubles and structs.

NOTE: The cast is actually optional! int *p = 0; is also valid!

Dynamic Storage

To use any of the following functions, you must #include <stdlib.h>.

stdlib.h defines the following function: void *malloc(size_t size)
malloc returns a pointer to a block of size bytes of memory

void free(void *p) is malloc‘s inverse.
free releases the memory allocated by malloc
NOT FREEING MEMORY WILL LEAD TO MEMORY LEAKS, WHICH ARE BAD

How are these functions useful?
Well, let’s look at an example:

    #include <stdlib.h>
    int *numbers(int n) {
        int *p = (int *)malloc(n * sizeof (int));
        for (int i = 0; i < n; i++)
            p[i] = i + 1;
        return p;
    }

This little function returns a pointer to an array filled with a range of numbers [0,n]

Lecture 21

Nov 6th

Dynamic Storage Continued

Let’s actually call numbers() from a main:

    void main () {
        int *q = numbers(100);
        printf("%d\n", q[50]); // Outputs 51
        free(q);
    }

Strings

How does C handle strings?
Well, simply put, a string in C is just an array of chars that is terminated by a null character (‘\0’).

We can define strings in a few ways:
1) char s[] = "hello";
2) char s[] = {'h','e','l','l','o','\0'};
3) char *s = "hello";

Each of these is equally valid (although 2 is usually not used).

String manipulations in C

Unlike high level languages, C has pretty bad built in string manipulation.
And by bad, I mean it doesn’t have any.
If you want to modify a string in some way, you have to manually write a function that will do an operation you like (or use a library like <string.h>).

As an example, let’s write a function that counts how many times a given character c occurs in a string s

c_count.c

    #include <stdio.h>

    int count(char *s, char c) {
        int count = 0;
        for (int i = 0; s[i] != '\0'; i++) {
            if (s[i] == c) count++;
        }
        return count;
    }

    //// you can also rewrite the for loop with pointers
    // for (char *p = sl *p != '\0'; p++) {
    //     if (*p == c) count++;
    // }

    void main() {
        char *hi = "Hello world!";
        printf("%d\n",count(hi,'l')); // 3
        printf("%d\n",count(hi,'z')); // 0
        printf("%d\n",count(hi,'L')); // 0
    }

string.h

<string.h> is a helpful C library that implements some basic string manipulation and utility functions.

Here is a list of some helpful functions from the library:

size_t strlen(const char *s);
- returns the string length of s in an unsigned long
- does not include '\0'
- const means that strlen should only read the string, not mutate it.
char *strcopy(char *s0, const char *s1);
- copies string s1 into s0
- returns s0
- s0 must have enough room to store the contents of s1
  - strcopy does NOT check that there is enough room
  - if there is not enough room, strcopy will just overwrite any bits that follow after s0
char *strcat(char *s0, const char *s1);
- concatenates s1 to s0(adds s1 to the end of s0);
- returns s0
- Again, it doesn not check there is enough room, like strcopy
- Why does it return a pointer? Because one could “chain” multiple strcats to concat multiple strings together in a one line expression
int strcmp(const char *s0, const char *s1);
- computes strings “lexicographically,” i.e: comparing ASCII values
- returns:
  - < 0 if s0 < s1
  - ==0 if s0 == s1
  - > 0 if s0 > s1
- Example:
  - printf("%d\n", strcmp("abc","abC")); returns 0 + 0 + (99-67) = 32

Let’s write a new version of strcat that dynamically allocates enough memory to hold the contents of s0 and s1

concat.c

    #include <stdlib.h>
    #include <string.h>

    char *concat(const char *s0, const char *s1) {
        char *s = (char*)malloc((strlen(s0) + strlen(s1)) + 1);
        // fine since sizeof(char) is just 1
        // extra 1 is there for the `\0`
        strcpy(s,s0);
        strcat(s,s1);
        return s;
    }

    void main() {
        char *hi = concat("hello", "world");
        printf("%s\n", hi);

        free(hi);
    }

Now, for something completely different:

Switch Statements

Switch statements are an alternative to if statements.
They are not as versitile, but they may improve code readability

Switch statements are comprised of a few base parts:

    switch (expression) {  // evaluate expression
        case expr1:        //   if expression has a value expr1...
            statements...  //     do statements...
            break;         //     end switch
        case expr2:        //   if expression has a value expr2...
            statements...  //     do statements...
                           //     (no break, therefore fall through to next case)
        default:           //   if none of the above
            statements...  //     do statements...
    }

For example, we could write a program that prints out a standing based on a letter grade:

    void standing(char grade) {
        switch (grade){
            case 'A': printf("EXCEL\n"); break;
            case 'B': printf("GOOD \n"); break;
            case 'C': printf("SAT  \n"); break;
            case 'D': printf("POOR \n"); break;
            case 'F': printf("FAIL \n"); break;
            default : printf("INVALID\n");
        }
    }

Lecture 22

Nov 9th

Switch Statements cont.

Not including a break; at the end of a case will result in a “fall through” to the next case.
As an example, we can write a function that takes a letter grade and prints “pass” or “fail”

    void passFail(char grade) {
        switch (grade) {
            case 'A':
            case 'B':
            case 'C':
            case 'D': printf("pass\n"); break;
            case 'F': printf("fail\n"); break;
            default: printf("invalid\n");
        }
    }

Dynamic Storage

What important functions does #include <stdlib.h> give us access to?

void *malloc(size_t size);
- Allocates size bytes of memory for use by the program
void free(void *p)
- Frees up the memory previously allocated by the program
void *realloc(void *p, size_t size)
- Given a pointer to a dynamically allocated memory block (i.e: one returned by malloc or calloc), realloc will either expand or shrink that block of memory to size size
- If there is not enough room to expand the memory block, realloc may allocate a new block of memory elsewhere in the memory, and copy over data from the original block
- Returns pointer to new location of memory array (may or may not be equal to the given pointer, depends if ‘realloc’ allocated new memory and copied, or not)
void *calloc(size_t nmemb, size_t size);
- Allocates space for an array of nmemb elements of size bytes each, and initialtes all members of the array to 0

Note: malloc, calloc, and realloc all return 0 if they cannot allocate enough memory requested, or size == 0

We should check the return values of these functions to make sure they were successful by doing something like assert(p); when allocating to a pointer p

Pointers to Structs

What happens if we want tomalloc a memory block to hold structs?
Well, it works fine, but there is a weird syntax…
Take the following example:

    typedef struct {
        int hour, min;
    } tod;

    tod *t = malloc(sizeof(tod));

    // to reference the elements of the tod malloc'ed array,
    // we either do:

    (*t).hour = 18;

    // but that's ugly, so the more common way is

    t->hour = 18;

Better Arrays

Wouldn’t it be great if C had a vector type that

grows automatically when adding new elements?
knows the ammount of elements it contains?
initializes it’s own elements to 0?

Yeah it would! So let’s make one!

We can make a special struct that has 3 fields:
1) a - the array of vector elements
2) length - the number of vector elements in the array
3) size - The total number of elements that have been allocated in the array

First, let’s come up with an outline for what functions we want…

vectors.h

    #ifndef VECTOR_H
    #define VECTOR_H
        struct vector;
        typedef struct vector vector;

        vector *vectorCreate();
        vector *vectorDelete(vector *v);
        void vectorSet(vector *v, int index, int value);
        int vectorGet(vector *v, int index);
        int vectorLength(vector *v);
    #endif

Small note: we do not explicitly state what struct vector stores here in the header, and we instead declare it’s structure later on in our implementation file vector.c.
This practice is called opaque structs, i.e: we make it so that the user doesn’t see the details of your struct implementation in the header file.

Alright! Now, what behavior do we expect from using these functions?

vector_test.c

    #include <stdio.h>
    #include "vector.h"

    void main() {
        vector *v = vectorCreate();

        vectorSet(v, 10, 2);
        printf("%d\n", vectorLength(v));    // 11
        printf("%d\n", vectorGet(v, 10));   // 2
        v = vectorDelete(v);
    }

Now, let’s actually implement the functions!
JKLOLNO We ran out of time. TUNE IN NEXT LECTURE FOR MORE EXCITING C IMPLEMENTATIONS!

Lecture 23

Nov 11

Okay, here is the actual implementation:

vectors.c

    #include <assert.h>
    #include <stdlib.h>
    #include "vector.h"

    struct vector{
        int *a;
        int length, size;
    };

    vector *vectorCreate() {
        vector *v = malloc(sizeof(vector));
            assert(v);
        v->size = 1;
        v->a = malloc(1*sizeof(int));
            assert(v->a);
        v->length = 0;
        return v;
    }

    vector *vectorDelete(vector *v) {
        if (v) {
            free(v->a);   // Free array in v
            free(v);      // Free the struct v
        }
        return 0;         // sets pointer to 0
    }

    void vectorSet(vector *v, int index, int value) {
        assert(v && index >= 0);
        // grow storage if necessary
        if (index >= v->size) {
            do {
                v->size *= 2;
            } while (index >= v->size);
            v->a = realloc(v->a, v->size * sizeof(int));
        }
        // another way to do this is to increase
        // the size of the array using
        //     v->size = 1<<ceil(log(index)/log(2));
        // but just because you can, doesn't mean you should

        // now, fill new elements with 0s
        while (index >= v->length) {
            v->a[v->length] = 0;
            v->length++;
        }
        v -> a[index] = value;
    }

    int vectorGet(vector *v, int index) {
        assert(v && index >= 0 && index < v->length);
        return v->a[index];
    }

    int vectorLength(vector *v) {
        assert(v);
        return v->length;
    }

Information Hiding

Remember how we made it so that vector‘s srtucture was not declared in the header?
This design principle is called information hiding

Why do we practice this notion of information hiding?

If we hide the details of implementation from the user, yet keep the “interface” the same, we can change our implememntation without braking other people’s reliant code
If they can see your struct, they may directly reference it, and then when you change it’s implementaion, their code will break.

Big O Notation

Get ready for some Math!

Let $f(x)$ be a function over the real numbers.

$O(f(x))$ is a set of functions such that: $g(x) \in O(f(x))$ if and only if there exists an $M>0$ and $x_0$ such that $|g(x)| \leq M|f(x)|$ for all $x > x_0$

In pure math:

$g(x) \in O(f(x)) \Longleftrightarrow \exists\ M>0, x_0\ s.t\ |g(x)|\leq M|f(x)| \ \forall\ x > x_0$

For example:

$3x^2 + 2 \in O(x^2)$

Proof:
if $x>1$ , then if $M = 5$

$|3x^2 +2 | = 3x^2 + 1 \leq 5x^2 = 5|x^2|\\ x_0 = 1$

Therefore, if $x_0 = 1, M = 5$

$|3x^2 +2 | = M|x^2|$ for all $x > x_0$

Another example of a Constant function

$6sin(x) \in O(1)$

Proof:
if $x>0, M=6$ , then $|6sin(x)| \leq 6$

Polynomials of degree $n$ belong to $O(x^n)$ .
Proof:
if $x > 1$ ,

$|a_nx^n+a_{n-1}x^{n-1}+...+a_0 \\ \leq |a_n|x^n + |a_{n-1}|x^{n-1}+...+|a_0| \\ \leq (|a_n| + |a_{n-1}|+...+|a_0|)x^n$

This holds if $x_0 = 1, M = \sum\limits_{i=1}^n|a_n|$
As a result, if $n \leq m$ then $x^n \in O(x^m)$

Lecture 24

Nov. 13

Big O Notation Continued

More examples! Here is a Logarithmic function:

$log_a(x) \in O(log_b(x))$

Proof:
if $x > 1$ ,

$|log_a(x)| = |log_b(x)|\\ = \frac{log_b(x)}{log_b(a)}\\ = \frac{1}{log_b(a)}|log_b(x)|\\$

Therefore, if $x_0 = 1, M = \frac{1}{log_b(a)}$

i.e: we can ignore the base of a logarithm

We rarely write the bse of the logarithm in Big O Notation

One last example: Exponential functions:

$x^n \in O(c^x)$ if $n$ is an int, and $c > 1$

Combinations of Big O’s

if $g_0(x) \in O(f_0(x))$ and $g_1(x) \in O(f_1(x))$ , then
i) $g_0(x) + g_1(x) \in O(f_0(x)+f_1(x))$
ii) $g_0(x)g_1(x) \in O(f_0(x)f_1(x))$

Transitivity of Big O’s

if $h(x) \in O(g(x))$ and $g(x) \in O(f(x))$ , then

$h(x) \in O(f(x))$

A note on convention:

$g(x) \in O(f(x))$

can also be written as:

$g(x)$ is $O(f(x))$

$g(x) = O(f(x))$

Big O Notation in CS

How is Big O Notation relevant in CS?
Well, we can use it to analyze the efficiency of algorithms!

Take the following Linear Search Algorithm:
It returns the index of the first occurance of a value in an array.

    int search(int a[], int n, int value) {
        for (int i = 0; i < n; i++) {
            if (a[i] == value) return i;
        }
        return -1; // value not found
    }

What operations does this function perform?

Order	Operation	Time to Perform
1	enter the function	up to A
	start the loop
2	test the loop condition	up to B n times
	evaluate if expression
	increment loop counter
3	return answer	up to C

Assuming n > 0:

The best case scenario is that the value is found in a[0].
Time $= A + B + C = O(1)$ , or constant time.

The worst case scenario is that the value is not found.
Time $= A + Bn + C = O(n)$ , or linear time.

The average case is that the value is located somewhere between a[0]…a[n-1]
Time $= \frac{1}{n} \sum\limits_{i=1}^n(a+Bi+C)\\ = A + B + \frac{B}{n} \sum\limits_{i=1}^n(i)\\ = A + C + \frac{B}{n}\frac{n(n+1)}{2} \\= A + C + \frac{B}{2} + \frac{B}{2}n\\ = O(n)$
or linear time.

Usually, we are only interested in the worst case scenario.

Jargon!

Sorted from leat to most complex:

Big O	Name
$O(1)$	constant time
$O(log n)$	logarithmic
$O(n)$	linear
$O(n^2)$	quadratic
$O(n^3)$	cubic
$O(n^m)$	polynomial
$O(c^n)$	exponential
$O(n!)$	factorial
$O(n^n)$	write a new algorithm

Lecture 25

Nov 16th

Sorting

Given an array of integers, how can we sort the array in ascending order (non-descending order)?

Relevant Interesting Video:
https://www.youtube.com/watch?v=kPRA0W1kECg

Sorting - Selection Sort

Find the smallest element
Swap with first element
Repeat above with the rest of the array, finding next smallest number, and swapping with next element

selection.c

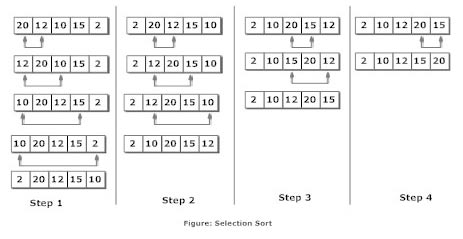
    #include <stdio.h>

    void selection_sort (int a[], int n) {
        for (int i = 0; i < n-1; i++) {
            int min = i;
            for (int j = i+1; j<n; j++)
                if (a[j] < a[min]) min = j;

            int temp = a[min];
            a[min] = a[i];
            a[i] = temp;
        }
    }

    void main (){
        int a[] = {-10,-7,2,14,11,38};
        int n = sizeof(a)/sizeof(a[0]);

        selection_sort(a,n);

        for (int i = 0; i < n; i++) {
            printf("%d, ", a[i]);
        }
        printf("\n");
    }

This is a $O(n^2)$ algorithm. Why? Well, let’s analyze it…

Entering the function, and initializing the outer loop will take A Time.
In the outer loop:
- Setting up the inner loop, swapping the variables, and running the inner loop takes B * (n - 1) Time.
- In the inner loop:
  - finding the smallest number will take C * (n - (i + 1))

Thus, the total execution time will be:

$A + B(n-1) + C( (n-1)+(n-2)+(n-3)+...+1 ) \\ = A + B(n-1) + C \sum\limits_{i=1}^n(i) \\ = A + B(n-1) + C\frac{n(n-1)}{2}\\ = O(n^2)$

Sorting - Insertion Sort

seperate the array into a sorted part and an unsorted part.
for every x in the unsorted part, find where x should go in the sorted part.
- shift up elements that are > x in the sorted part
- insert x
repeat n-1 times

insertion.c

    #include <stdio.h>

    void insertion_sort (int *a, int n) {
        int i, j, x;
        for (i = 1; i < n; i++) {
            x = a[i];
            for (j = i; j > 0 && x < a[j - 1]; j--) {
                a[j] = a[j - 1];
            }
            a[j] = x;
        }
    }

    void main (){
        int a[] = {-10,2,14,-7,11,38};
        int n = sizeof(a)/sizeof(a[0]);

        insertion_sort(a,n);

        for (int i = 0; i < n; i++) {
            printf("%d, ", a[i]);
        }
        printf("\n");
    }

This is also a $O(n^2)$ algorithm, but it can be $O(n)$ sometimes!

Outer loop has n-1 interations
Inner loop has 0 -> i iterations
In the worst case:
- time $= 1 + 2 + 3 + ... + (n-1) = O(n^2)$
In the best case though:
- time $= (n-1)C = O(n)$

Lecture 26

Nov 18

Sorting - Merge Sort

Unlike the above algorithms, merge sort is a divide and conquer algorithm.
It is also a recursive algorithm

Divide the array in half
Sort each half (recursively)
Merge the results

merge.c

    #include <stdio.h>
    #include <stdlib.h>
    #include <assert.h>

    // a is array to be sorted
    // t is temp array
    // n is size
    void merge_sort (int a[], int t[], int n) {
        if (n <= 1) return;

        // divide and sort both halves
        int middle = n / 2;
        int *lower = a;
        int *upper = a + middle;

        merge_sort(lower, t,     middle);
        merge_sort(upper, t, n - middle);

        // merge the halves:
        int i = 0;      // lower index
        int j = middle; // upper index
        int k = 0;      // temp  index

        // One half...
        while (i < middle && j < n) {
            // lower < upper
            if (a[i] <= a[j]) t[k++] = a[i++];
            // lower > upper
            else              t[k++] = a[j++];
        }

        // Other half...
        // Only one of the two loops below will
        // actually execute
        while (i < middle) t[k++] = a[i++];
        while (j < n)      t[k++] = a[j++];

        // copy from temp to a
        for (i = 0; i < n; i++) a[i] = t[i];

    }

    void sort(int a[], int n) {
        int *t = malloc(n*sizeof(int));
            assert(t);
        merge_sort(a, t, n);
        free(t);
    }

    void main (){
        int a[] = {-10,2,14,-7,11,38};
        int n = sizeof(a)/sizeof(a[0]);

        sort(a,n);

        for (int i = 0; i < n; i++) {
            printf("%d, ", a[i]);
        }
        printf("\n");
    }

What is the time complexity of this algorithm?
Well, it’s actually $O(n log(n))$ !
Why?

Suppose $n = 2^k$
So, $n = \{2,3,8,16...\}\ k = \{1,2,3,4...\}$
The size of the array is divided in half $k = \log_2(n)$ times, and ech time it is split, $n$ operations are done on that level.

So: $O(nk) = O(n\log_2(n)) = O(n\log(n))$

This is best, worst, and average all at once.

Lecture 27+28

Nov 18

Sorting - Quicksort - WARNING, BAD NOTES

Tony Hoare invented this alogrithm in 1959, when he was only ~26 years old!

“If you haven’t done anything worthwhile in CS before you turn 30, you probably never will”
- Prof. Andrew Morton

This is a good algorithm because you don’t have to use a temporary array!

How does quicksort work?

Pick an element of the array at random. We call this element P, the pivot element
We then partition the array into 3 sections, one of all element before P, P itself, and every element after P.
We then recursively sort each section other than P itself.

How do we actually partition? That’s the critical question…

One that these notes cannot adequately answer!
Sorry about that.
You really need diagrams for this one…
On the bring side, Wikipedia.org exists. And Google too!

While I can’t expain the algorthm, I can at least give you an implementation:

quick.c

    #include <stdio.h>
    #include <stdlib.h>
    #include <assert.h>

    // swap helper
    void swap(int *a, int *b) {
        int t = *a;
        *a = *b;
        *b = t;
    }

    void quick_sort(int a[], int n) {
        if (n <= 1) return;

        // sweep
        int m = 0;
        for (int i = 1; i < n; i++) {
            if (a[i] < a[0]) {
                m++;
                swap(&a[m],&a[i]);
            }
        }

        // put pivot between partitions
        // i.e, swap a[0] and a[m]
        swap(&a[0],&a[m]);

        // quicksort each partition
        quick_sort(a, m);
        quick_sort(a + m + 1, n - m - 1);
    }

    void main (){
        int a[] = {-10,2,14,-7,11,38};
        int n = sizeof(a)/sizeof(a[0]);

        quick_sort(a,n);

        for (int i = 0; i < n; i++) {
            printf("%d, ", a[i]);
        }
        printf("\n");
    }

Again, I’m not very good at explaining this one, so here is the takeaway:
This algorithm’s time efficiency is:

Best case $O(n\log(n))$
On average $O(n\log(n))$
Worst case (the array is already sorted) $O(n^2)$

Despite quicksort’s pretty bad worst case compared to other algorithms, in most cases, quicksort is still faster.

Also, I missed space complexity, sorry.

Lecture 29

Nov 23th

Quicksort Improvements

The Hoare partitioner is one way to make quicksort more efficient.
It’s uglier code, but it has better preformance.

Pick a Pivot
Sweep from left AND right
- using i and j to index left and right respectively
swap when a[i] > P && a[j] < P
stop when i > j

quicksort_hoare.c

    #include <stdio.h>

    void swap(int *a, int *b) {
        int t = *a;
        *a = *b;
        *b = t;
    }

    void quicksort(int a[], int left, int right) {
        int i = left, j = right;
        int pivot = a[left];

        while(i <= j) {
            while(a[i] < pivot) i++;
            while(a[j] > pivot) j--;
            if(i <= j) {
                swap(&a[i],&a[j]);
                i++; j--;
            }
        }

        if(left < j) quicksort(a, left, j);
        if(right > i) quicksort(a, i, right);
    }

    int main() {
        int a[] = { 2, -10, 14, 42, 11, -7, 0, 38 };

        quicksort(a, 0, sizeof(a)/sizeof(a[0]) - 1);

        for (int i = 0; i < sizeof(a)/sizeof(a[0]); i++) {
            printf("%d, ", a[i]);
        }
        printf("\n");

        return 0;
    }

The qsort Function

In stdlib.h there is a function called qsort that is defined as follows:

void qsort(void *base, size_t n, size_t, size, int (*compare)(const void *a, const void *b));

*base is a pointer to the first element in the array
n is the number of elements in the array
size is the size of each array element in bytes
*compare is a function pointer to some function that
- returns < 0 if *a < *b
- returns 0 if *a = *b
- returns > 0 if *a > *b

Essentially, qsort is a heneralized sorter that can sort any structure you give if so long as you specify the type of structure you are passing it, and how to comapre structure elements.

For example, you can tell qsort to sort integers by doing something like this:

    #include <stdlib.h>

    int compare(const void *a, const void *b) {
        int p = *(int *)a;
        int q = *(int *)b;
        if (p < q) return -1;
        else if (p == q) return 0;
        else return 1;
    }

    void sort(int a[], int n) {
        qsort(a,n,sizeof(int),compare);
    }

And you can just call sort()

Lecture 30

Nov 27th

Fibonacci Numbers

Fibonacci numbers are defined as follows:

$F_0 = 0\\ F_1 = 1,\\ F_n = F_{n-1}+F_{n-2}$

In C:

fibonacci.c

    // prints 10th fibonacci number
    #include <stdio.h>

    int fib (int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        return fib(n-1)+fib(n-2);
    }

    int main () {
        printf("%d\n",fib(10));
        return 0;
    }

Also, there is no easy way to get to this result, but the time complexity of this particular algorithm is $O(2^n)$ . Which is bad. Real bad.

A better implementation of fibonacci would be as follows (it is only $O(n)$ )

    int fib2(int n) {
        int m = 1;
        int k = 0;
        int i;

        for (i = 1; i <= n; i++) {
            int tmp = m + k;
            m = k;
            k = tmp;
        }
        return m;
    }

Hint. You need this for the exam.

Measuring program runtime

Say we want to measure how long it takes to for a certain function / program to run?
In C, a simple way to implement such a measurement is to use time.h‘s clock() funcion to get the “time” at the start of the thing you want to measure, and once more at the end.

NOTE: “time” is not real time usually, it’s some sort of “number of ticks” since some arbitrary event.

For example, say we want to measure out fib() function above:

    #include <stdio.h>
    #include <time.h>

    // this is implicitly defined
    // #define CLOCKS_PER_SEC 100000

    int fib (int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        return fib(n-1)+fib(n-2);
    }

    int main () {
        clock_t start = clock();
        printf("%d\n", fib(37));
        clock_t end = clock();
        printf("%ld\n", (long int)(end-start)/CLOCKS_PER_SEC);
        return 0;
    }

Binary Search

How can we efficiently search through a sorted array?

We can use a binary search algorithm!

Probe the middle element
- if a[m] > value, search left half
- if a[m] < value, search right half
- if a[m] == value, return m

Let’s make a function int search(int a[], int n, int value) that will return the position of the element if it is found in the array, or -1 otherwise:

binarysearch.c

    #include <stdio.h>

    int search(int a[], int n, int value) {
        int l = 0,
            h = n-1;

        while (h >= l) {
            int m = l+(h-l)/2; // or (h+l)>>1; becuase bitshifting
            if (a[m] == value) return m;
            if (a[m] < value) l = m+1;
            if (a[m] > value) h = m-1;
        }

        return -1;
    }

    int main() {
        int a[] = {-10,7,0,2,11,14,38,42};
        printf("%d\n", search(a,sizeof(a)/sizeof(a[0]),10));    // -1
        printf("%d\n", search(a,sizeof(a)/sizeof(a[0]),2));     // 3
        printf("%d\n", search(a,sizeof(a)/sizeof(a[0]),42));    // 7
        return 0;
    }

Evidently, the Worst Case time complexity is $O(\log(n))$ and the Best Case time complexity is $O(1)$ (the midpoint is the correct element)

Lecture 31+32

Nov 30th - Dec 2nd

A Summary of Sorting Algorithms

Algorithm	Best Time	Worst Time	Extra Memory?
Selection	$O(n^2)$	$O(n^2)$	No
Insertion	$O(n^2)$	$O(n)$	No
Merge	$O(n\log(n))$	$O(n\log(n))$	Yes
Quick	$O(n\log(n))$	$O(n^2)$	No

NOTE: THIS IS THE END OF MATERIAL COVERED BY THE FINAL EXAM

Linked Lists

Recall our vector implementation, and how as the number of vectors outgrew the size of the array, the array doubled in size.
This could be inneficient for frequent insertions mid list (for sparsley used vectors).
Is there a better way of implementing an expanding array-like data structure?

Well, obviously. It’s called a linked list!

We will implement a linked list to hold polynomials (vectors are done in an upper year CS course)

So, let’s say we want to store information about the polynomial 2x³ + 8x - 12
We can make a struct with 3 properties:
1) double The coefficient
2) int The degree
3) *poly A pointer to the next element of the polynomial (NULL if end of the list)

poly.h

    #ifndef POLY_H
    #define POLY_H

    typedef struct poly {
        double coeff;
        int deg;
        struct poly *next;
    } poly;

    poly   *polyCreate      ();
    poly   *polyDelete      (poly *p);
    poly   *polySetCoeff    (poly *p, int deg, double coeff);
    double  polyEval        (poly *p, double x);
    int     polyDegree      (poly *p);
    poly   *polyReverse     (poly *p);

    #endif

main.c

    #include <stdio.h>

    #include "poly.h"

    int main() {
        poly *p = polyCreate();

        p = polySetCoeff(p, 3, 3.0);
        p = polySetCoeff(p, 0, 3.0);
        p = polySetCoeff(p, 1, 3.0);

        printf("%g\n", polyEval(p,-1)); // -3

        p = polyDelete(p);

        return 0;
    }

poly.c

    #include <math.h>
    #include <stdlib.h>

    #include "poly.h"

    poly *polyCreate() {
        // init empty list
        return 0;
    }

    poly *polyDelete(poly *p) {
        while (p) {
            poly *t = p;    // set to to point to p
            p = p->next;    // set p to point to next element in ll
            free(t);        // free origional p value
        }
        return p;
    }

    // Notice that p is passes *by value*
    // so we can increment and modify p within this loop
    // to our heart's content
    double polyEval(poly *p, double x) {
        double f = 0.0;     // value of the function

        // iterate over the nodes(terms) and evaluate each appropriately
        // Note: DO NOT USE p++! 
        // Terms are (probably) not next to one another in memory
        for (; p; p = p->next)
            f += pow(x,p->deg)*p->coeff;

        return f;
    }

    poly *polySetCoeff(poly *p, int deg, double coeff) {
        // ignore requests to set coeff to 0
        if (!coeff) return p;

        // if empty list / insert at head
        if (!p || deg > p->deg) {
            poly *q = malloc(sizeof(poly));
            q->coeff = coeff;
            q->deg   = deg;
            q->next  = p;
            return q;
        }

        // find location to insert
        poly *cur = p;
        for (; cur->next && cur ->next->deg > deg; cur = cur->next);
        // this for loop brings us to the correct place

        // If we are not at the end of the list, and it is the same
        // degree as the degree we want to set the coefficient of...
        if (cur->next && cur->next->deg == deg) {
            cur->next->coeff = coeff;
        } 
        // If we are at the end of the list, or there does not exit
        // a node for the desired degree...
        else {
            poly *q = malloc(sizeof(poly));
            q->coeff = coeff;
            q->deg = deg;
            // insert into the list (order of operations matters!)
            // first, set q's next pointer to point to cur's next
            q->next = cur->next;
            // next, set cur's next point to point to q
            cur->next = q;
        }
        return p;
    }

    // calculate degree of polynomial
    int polyDegree (poly *p) {
        if (p == 0) return 0;   // behavior agreed upon beforehand
        return p->deg;          // because ll are listed automagically
    }

    // reverse a linked list
    // THIS BREAKS OTHER FUNCTIONS
    // IT'S JUST A GENERAL IMPLEMENTATION
    // THEY ASK THIS ON INTERVIEWS
    poly *polyReverse(poly *p) {
        poly *q = 0; // reverse list that starts empty
        while(p) {
            // remember p->next
            poly *next = p->next;
            // insert the next node of the old list
            // into the head of the reversed list
            p->next = q;
            q = p;
            p = next;
        }
        return q;
    }

Lecture 33

Dec 2nd

Makefiles

Why type long commands to compile programs when you can just make a makefile, type make into your terminal, and boom bam alakazam, your program is compiled!

Lets make a Makefile for our poly linked list program:

Makefile

    poly: main.c poly.c poly.h         # target: prerequisites
        gcc -o poly poly.c main.c -lm  # recipe
    clean:
        rm -f poly

Here is another Makefile…

Makefile

    # Variables
    CC = gcc
    CFLAGS = -g -std=c99                 # -g for debugging info
    LIBS = -lm

    default: poly
    cplex: cplexMain.c cplex.c cplex.h
    poly: main.c poly.c poly.h
    %:%.c
        $(CC) $(FLAGS) -o $@ $^ $(LIBS)  # $@ is target name
    PHONY: clean
    clean:
        rm -f foly cplex

How does this thing work? Great question reader, one that I would love an answer to!
This is just what Morty wrote verbatim

Random sidenote!

There is a little difference between the following two lines:

    const char *c;
    char * const c;

Line one states that we cannot modify the value that the pointer c points to.
Line two states that we cannot modify the actual pointer c.

What’s on the exam?

Know the following aspects of the language:

Fundamentals (vars, types, expressions, if else, loops, switch, printf scanf, etc)
- Ch. 2-7 | think quiz 1
Arrays and Initializers
- Ch. 8.1
Pointers, arrays, pointer arithmetic
- Ch 11-12
Strings, strlen, strcpy, strcat, strcmp
- Ch. 13
Header files (how to do seperate compilation)
- Ch. 15
Structures (params, return types, arrays of / within structs)
- Ch. 16.1, 16.2
Dynamic Memory (malloc, free, realloc, calloc), function pointers, qsort
- Ch. 17.1-17.4,17.7
math.h
- Ch. 23.3
assert.h
- Ch. 24.1
Unicode
- Ch. 25.2

Know the following algorithms:

Euclid’s Algoritm (GCD)
Sieve of Eratosthenes (primes)
Horner’s Method (eval. polynomials)
Bisection (root finding)
Pagerank (fixed-point iteration) FORMULA GIVEN
Sorting:
- Selection
  - best = worst = O(n²)
- Insertion
  - best = O(n), worst = O(n²)
- Merge Sort
  - best = worst = O(n log(n))
- Quicksort (only need to memorize one partitioner) (assume p=a[0])
  - best = (n log(n))
  - worst = O(n²)
Searching
- Linear
  - O(n)
- Binary
  - O(log(n))
Fibonacci Sequence (Linear)

Other stuff:

Rounding
Big O (How to compute and which are fastest)

Format of the exam

Closed Book, no Calculators
20-26 questions, 4 marks each

Before each question, there will be a collection of symbols that mark what type of material the question covers (i.e: A for assert, B for Bisection, etc…)

Exam Review

Question 1

The quicksort algorithm has three steps:
1) pick a point, 2) partiton the array, 3) sort each partition recursively

Let int a[0] = {5,6,4,7,3,8,2}

If a[0] is the pivot, show a[] after initial partitoning

Answer 1

    5,6
    5,4,6
    5,4,6,7
    5,4,3,7,6
    5,4,3,7,6,8
    5,4,3,7,6,8,7
    2,4,3,5,6,8,7

Question 2

Approximately how many times will a binary search probe a sorted array of size 1mil when searching for a value that is not in the array?
A) 20
B) 1000
C) 2
D) 1mil
E) Binary search only works with unsorted array

Answer 2

It’s A.
2¹⁰ = 1024
2²⁰ = 1024*1024 approx 1mil

Question 3

The greek character zeta has the unicode codepoint value of 150 (decimal), which is 1110110110 in binary

What is the UTF-8 encoding of this character?

Answer 3

    110 01110 10 110110

Question 4

Recall that qsort is defined as
void qsort(void *base, size_t n, size_t size, int (*compare)(const void *a, const void *b));

Implement a function void sort(struct tod a[], int n) that invokes qsort to sort an array of time-of-day structs struct tod {int hour, minute;}
You will need to define the compare function.

Answer 4

    #include <stdlib.h>

    int compare(const void *_a, const void *_b) {
        struct tod a = (struct tod *) _a;
        struct tod b = (struct tod *) _b;
        return (60*a.hour + a.minute)
             - (60*b.hour + b.minute);
    }

    void sort(struct tod a[], int n) {
        qsort(a,n,sizeof(struct tod),compare);
    }

Question 5 - Harder end of the spectrum

Implement a function int zeroes(int n); that return the number of trailing zeroes at the end of n!. Assume n>=1.

Answer 5

Do it yourself!

That’s it. Good luck on the final.

Hope these notes helped :D
- Daniel Prilik