A Quest to Find a Highly Compressed Emoji :shortcode: Lookup Function
Have you ever wondered what’s the smallest amount of static storage (code + data) needed to map emoji :shortcodes: to emoji?
Probably not… but now that I’ve posed the question, aren’t you at least a little curious what the answer might be?
So hey, if you’ve got some time to spare, why not stick around a while and learn a bit about cool topics such as perfect hashing, probabilistic data structures, and 2D dynamic programming algorithms?
Take a break from solving whatever “important problem” you’re working on, kick back, relax, and join me on my [somewhat useless] quest to find a highly compressed emoji :shortcode: lookup function!

Thanks to the power of WebAssembly, you can play with the final result right from your browser!
—-> Check out the online demo! <—–
What even is a “Highly Compressed Emoji Shortcode Lookup Function”?⌗
Before embarking on our quest, we should probably clarify what it is we’re looking for exactly exactly.
We want to write a function that accepts shortcode strings as input, and outputs UTF-8 emoji as output:
// e.g: shortcode_to_emoji("flamingo") -> Some("🦩")
fn shortcode_to_emoji(input: &str) -> Option<&str>
At first glance, this doesn’t seem too difficult: just find a free, open source dataset of emoji shortcodes, load that data into memory, construct a hashmap, and start querying it - easy peasy!
Not so fast.
While that approach would work just fine on your fancy shmancy
Linux/Windows/macOS/TempleOS powered desktop computer, what if we wanted to run
this lookup function on something a little bit more… embedded? If we tried to
dynamically construct a hashmap at runtime on a tiny, resource-constrained
ARM/AVR microcontroller, we’d very quickly run out of dynamic memory (assuming
something like malloc is even available on said platform).
Indeed, therein lies the need for a “Highly Compressed” lookup function - if we want to run this code on an embedded system, the lookup function will have to occupy as little static storage (code and read-only data) as possible.
At this point, you might be thinking to yourself “who in their right mind would want to map emoji shortcodes on embedded hardware?” Fair enough! I’ve included my inspiration behind this wild endeavor in the next section.
Then again, if you’re mostly interested in the problem itself, feel free to skip ahead to Getting a feel for the Data.
💡 Inspiration 💡⌗
I’m a big fan of custom mechanical keyboards, as aside from looking and sounding awesome, they’re also an excellent hardware-hacking platform. Most custom mechanical keyboards use the open source QMK firmware, which comes with a host of built-in features for doing just about anything you’d want on a keyboard.
One particularly useful QMK feature is its ability to type Unicode characters. In a nutshell, you can program your keyboard such that when a certain key (or sequence of keys) is pressed, it will send whatever keystrokes are required to input Unicode on any of the several supported platforms. This is great, because it means that the 🅱 emoji is never more than a few keystrokes away!
One somewhat annoying limitation of QMK’s built-in Unicode support is that users are required to define which emoji they’d like to use ahead of time. While it’s not too difficult to find a set of “workhorse” emoji to preload onto the keyboard, it’d certainly be convenient to also be able to type more “bespoke” emoji when the need arises. Sure, quick and easy access to the 🅱 emoji is great and all, but what about those rare cases where I quickly need access to the 🦩 emoji? What am I supposed to do - use my OS’s built-in emoji picker like a peasant?? Never!
And so, I decided to spend my valuable free time on something some folks might call “a total waste of time”: writing a Rust library that exports a single function that can look up emoji shortcodes using the minimum amount of code + read-only data, and without requiring any heap allocation!
Now, without further ado, let’s dive into the implementation!
📝 Getting a feel for the Data 📝⌗
First things first, we’ll need a dataset of emoji shortcodes to work with. For this project, I decided to use the same emoji database as used by GitHub, since it’s the one I’m most familiar with, and it’s also readily available as a big ‘ol JSON blob. The particular dataset exhibits the following properties:
| total shortcode, emoji pairs | 1848 |
| raw shortcode character data | 18715 bytes |
| raw emoji UTF-8 character data | 11096 bytes |
| average shortcode length | 10.12716 bytes |
| average emoji length | 6.004329 bytes |
Converting this data set into a CSV file of raw shortcode,emoji pairs would
result in roughly ~34kb file. Aside from being a totally impractical data
structure for querying on an embedded system, 34kb is quite a bit of data in an
embedded context! Let’s see if we can do any better…
🛠️ Implementation 🛠️⌗
Since we know all the key-value pairs ahead of time, a good place to start off might be to generate a perfect hash map of shortcodes to emoji at compile time. Unlike typical hash functions, perfect hash functions guarantee that each individual valid input is mapped to a distinct index. This property means that there is zero wasted space in the underlying hash table.
In fact, the foundation of this entire project is the incredible
rust-phf, which I ended up heavy
modifying and optimizing for this specific use-case. That said, even without
doing any modifications, the base rust-phf crate results in ~100kb of
code + data overhead, and can be used on systems without dynamic allocation.
Now, 100kb doesn’t seem that bad, but when you consider that the raw dataset of shortcodes + emoji is only ~34kb, and the fact that most embedded platforms I’m targeting have at most ~256kb of flash ROM, it’s should be obvious that there’s plenty of room for improvement.
Not to spoil the ending, but by using the host of optimizations and data layout/representation tricks outlined in the next couple sections, that 100kb number ends up shrinking down to a measly ~20kb!
Trick 1 - Storing hashes of 🔑 keys 🔑 instead of the keys themselves⌗
Let’s start off with a guiding question:
Why do hash tables need to store both values and keys, even in situations where there’s never a need to iterate over key-value pairs in the map?
This question has a couple different answers, but the one most relevant to this discussion is that hash tables need a copy of the original key to prevent false positive lookups, whereby an invalid key returns an unrelated value.
A fundamental property of hash tables is that given a unlimited set of inputs (i.e: all possible strings), and a limited set of outputs (i.e: the ~2000 emoji in our data set), a hash collision is essentially guaranteed to happen. As such, hash tables need to employ some sort of collision resolution algorithm.
If hash tables didn’t have any collision resolution, just imagine what sort of chaos simple input errors might result in! A harmless spelling mistake while trying to input
😄, compounded with some spectacularly bad statistical chance, somehow results in🍆instead!Unlikely? Sure. But why even take the chance?
In our case, since we happen to be using a perfect hash function, the conflict resolution strategy happens to be incredibly simple: just include an additional check that compares the input key against the expected key at that particular index. With this one simple trick, the hash table can ensure that invalid inputs are rejected with 100% certainty!
But enough about how hash functions work in general, we have a problem we want to solve!
One key insight about our problem is that we are only even interested in looking up values, and don’t actually care about what the set of valid keys is.
This begs the question: Is there any way we could somehow avoid storing all the keys in their entirety?
At last, we arrive at our first trick: Instead of storing each shortcode key in
its entirety as a raw string (which would take up a lot of space, around
size_of(char*) + 10 bytes on average), just store a small secondary hash
of the key!
This trick results in some absolutely monstrous space savings, cutting the
~18kb of raw shortcode string data down to just ~4kb (i.e:
size_of(hash("input")) * num_shortcodes bytes, assuming a 16-bit hash).
Unfortunately, this trick doesn’t come for free, and brings with it a nasty side-effect: since the hash function only stores a hash of the key, the collision resolution algorithm stops being 100% accurate. Indeed, the lookup function ends up having an infinite number of “false positive” inputs 😱
Fortunately, it turns out that it’s possible to greatly reduce the number of “reasonable” false positives (“reasonable” in the sense that the input isn’t comprised on random gibberish characters) simply by increasing the number of bits used for the secondary hash.
Now, I’m no statistician, so I really can’t comment to the theoretical impact of using more/less bits to reduce false positives, but I can say that though some extensive empirical testing - both via automated testing and human trials (read: mashing random keys on my keyboard) - it seems that a 16-bit hash works almost perfectly. Heck, if you’re really worried about space, even a single byte hash works great!
And don’t just take my word for it - go and play around with the online demo and see how well this “imperfect” collision resolution algorithm actually works - it ought to be pretty difficult to find any “reasonable” false positive inputs.
Trick 2 - Storing emoji without the overhead of offsets or 👉 pointers 👈⌗
The typical way to store static strings within a map is to store pointers to
the strings, and storing the strings themselves somewhere else in read-only
memory. Unfortunately, in this particular situation, this naive way of storing
strings results in some substantial overhead, as aside from storing the raw
UTF-8 string data for each emoji, we also need to store a pointer to the
string + some way to mark the bounds of a string (either by storing the string’s
length, or by including a null terminator). Given that most emoji are only ~6
bytes long, a size_of(char*) + 1 overhead per entry is brutal.
In memory, this naive table layout would look something like this:
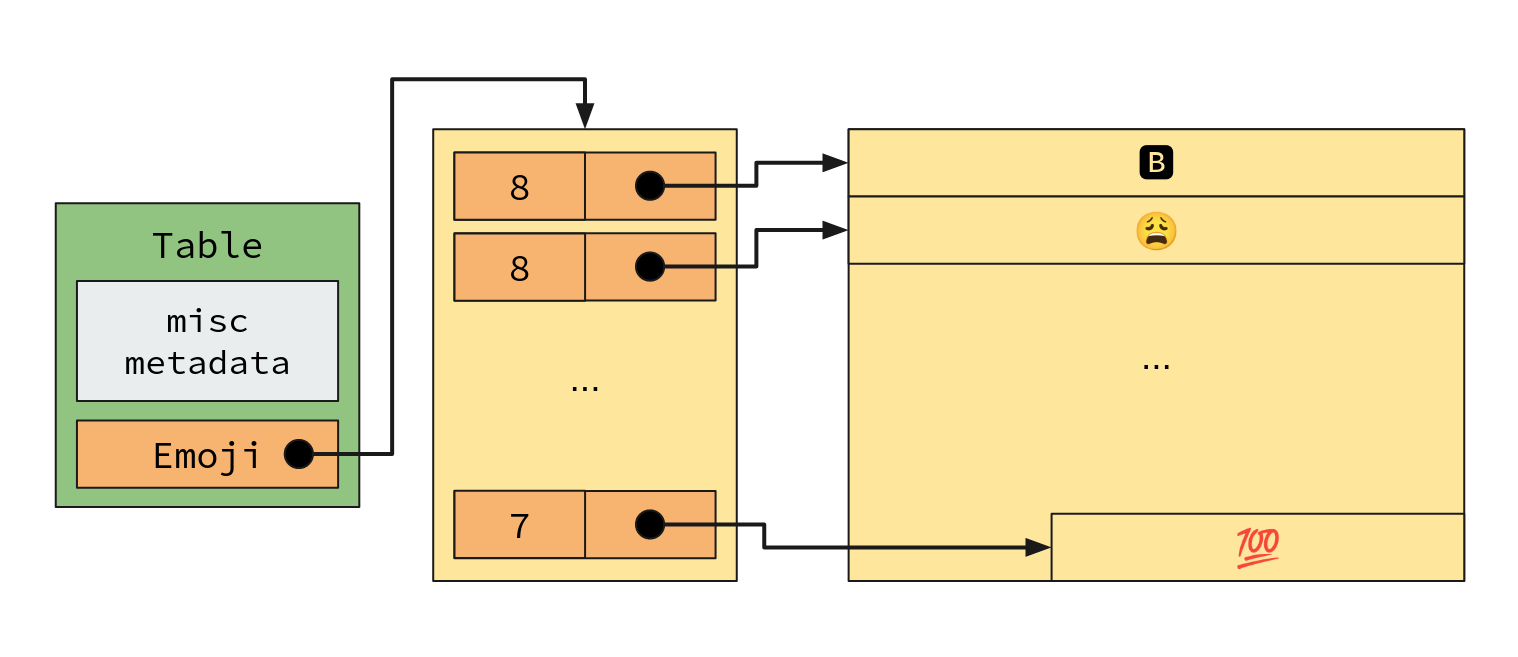
Total overhead:size_of(Table) + (Table.Emoji.len * (1 + size_of(char*))) + (raw emoji UTF8)
(Assuming string length is stored alongside the pointer)
Can we do any better? Absolutely!
Instead of generating a single map containing all the shortcode-emoji mappings,
n distinct maps are generated instead, one for each unique emoji string size.
With this setup, string data can be accessed directly, without requiring any
additional pointer indirection.
In memory, this smarter table layout would look something like this:
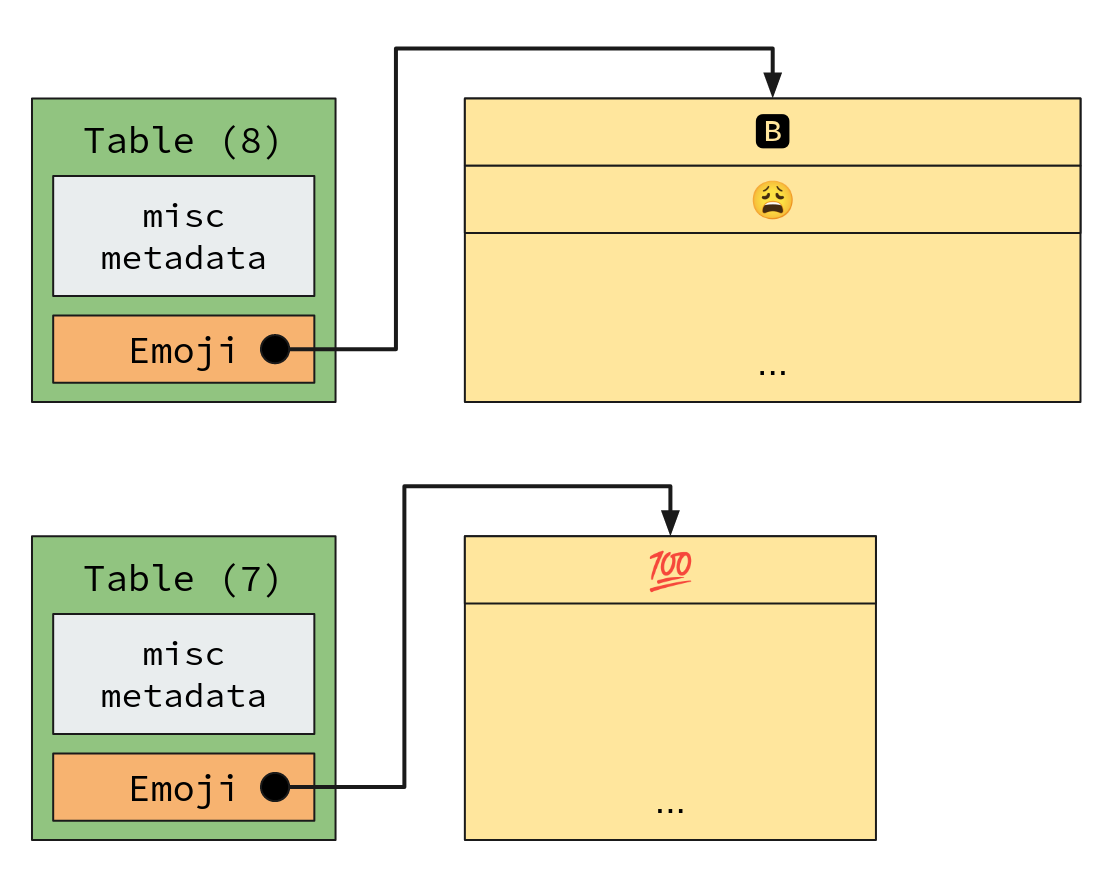
Total overhead:2 * size_of(Table) + (raw emoji UTF8)
Look at that! We totally cut out the Table.Emoji.len * (1 + size_of(char*))
overhead!
Of course, this optimization did require allocating a whole new table, which
does incur an additional size_of(Table) bytes of overhead, but if the table
contains a large number of values, then this extra overhead is negligible with
respect to the space saved by removing the pointer indirection.
Note: Now that there are multiple tables, the lookup function needs to be modified to iterate through all the tables, returning when a result is found. This is an easy fix to implement, though it can result in some problems down the line…
Trick 2.a - ✂️ Trimming Tiny Tables ✂️⌗
Content Warning: *Spicy* 2D Dynamic Programming Algorithms Ahead
Before covering the last major trick, I should mention an interesting optimization opportunity related to generating multiple tables:
For our particular emoji shortcode dataset, the following tables get generated:
| emoji len | entries |
|---|---|
| 3 | 64 |
| 4 | 1081 |
| 5 | 2 |
| 6 | 109 |
| 7 | 109 |
| 8 | 260 |
| 10 | 1 |
| 11 | 69 |
| 13 | 109 |
| 14 | 1 |
| 15 | 4 |
| 16 | 7 |
| 17 | 1 |
| 18 | 13 |
| 20 | 3 |
| 25 | 9 |
| 27 | 3 |
| 28 | 3 |
As it turns out, there are plenty of awkwardly-sized emoji in this data set. While most emoji tend to be in the 3-8 byte range, some emoji take up substantially more space. For example, the flag of Wales emoji (🏴) takes up a whopping 28 bytes!
This is quite unfortunate, as it requires generating whole new tables just for these occasional odd-sized emoji. This is undesirable for several reasons:
- Each table has some overhead associated with it, roughly
size_of(Table), which is ~64 bytes. For certain smaller tables, this overhead can be greater than the size of the data stored within the table itself! - The more tables there are, the more likely a hash-collision occurs while looking up entries deeper into the list. This will be covered in more detail in the Trick 3 section later on.
Suffice it to say, it’d be nice if we could somehow consolidate tables with fewer entries into their nearest-neighbors, thereby saving ourselves from requiring all these additional tables. As it turns out, it’s not actually that difficult to consolidate two tables into one - all it takes is a bit of null-padding!
Say we have a table that stores strings of length 3, containing
["foo", "bar", "baz"], and another table that stores strings of length 4,
containing just ["four"]. We can merge these two tables together by adding
some null-padding to each element in the first table, and then merging the two
tables together. The final result is a single table that stores strings of
length 4, containing ["foo\0", "bar\0", "baz\0", "four"].
As it turns out, finding the optimal order in which to merge tables is actually surprisingly tricky, and presents the opportunity for some interesting algorithm crafting. In fact, we can re-write this problem more abstractly as follows:
Consider a set of tables
T1..Tn, where each table storesmstrings of lengthn.Each table has a fixed overhead of
Kbytes associated with it.Given two tables
TaandTbwithmaandmbentries respectively, is it possible to consolidate the two tables into a single table by padding the strings contained within theT_min(a, b)table withmax(a, b) - min(a, b)“padding” bytes, and then merging the two tables into a singleT_max(a, b)table withma + mbentries.Q1. Find an algorithm that consolidates the tables that minimizes the total space used.
Q2. Find an algorithm that consolidates the maximum number of tables without introducing any additional space overhead.
The two questions optimize for the two different shortcomings listed above: space saving, and hash-collisions. Which of the two algorithms to use depends on the data set and what sort of properties you want the lookup function to have.
Now, truth be told, the algorithm that’s currently implemented in the library on GitHub is absolutely horrendous. I wrote it very late at night, and I’ve been too lazy to delete it + rewrite it ever since.
Thankfully, I happen to be friends with someone who’s pretty darn good at these sorts of algorithm questions, and managed to nerd snipe my friend Ethan Hardy into finding a really elegant and interesting solution to the problem.
Since I’m more of a “maker”-type software engineer rather than a “computer scientist”-type software engineer, I asked Ethan to describe the algorithm in his own words:
To fully optimize our space usage with these tables, we can employ the use of some dynamic programming techniques.
In a nutshell, we can iterate through a DP table storing solutions to subproblems restricted over two dimensions: which tables we have available, and which table must be the lowest-string-length unmerged table (unmerged here meaning not itself merged into another table; having tables with smaller strings merged into the table is ok).
Why this solution works is somewhat non-obvious, and the rationale behind the unmerged restriction is also fairly hard to describe… succinctly. All of this is to say that I’ve gone ahead and written a full, LaTeX typeset “white paper” that dives into the details of the algorithm.
You can read the full writeup by clicking on this link here.
- Ethan Hardy
I really recommend checking out Ethan’s writeup - it’s really cool seeing how dynamic programming can be used to solve a “real world” problem, as opposed to just contrived leetcode-style questions.
Trick 3 - Eliminate invalid mappings using 🎲 randomness 🎲 and fixup tables⌗
Unfortunately, there is a critical issue associated with using Trick #2 - using multiple maps may result in incorrect mappings for valid inputs. In the single-map approach, the properties of the PHF ensure that each valid input is mapped to a unique index, while in the multi-map approach, this property no longer holds, as valid inputs are also checked against hashmaps they aren’t in, opening the door for hash-collisions.
This is totally unacceptable, and has to be accounted for!
The approach I took was inspired by a bit of tech folklore from Naughty Dog studios: while working on the original Crash Bandicoot, the developers were having trouble fitting game assets into the PS1’s very limited memory. The solution they came up with? Writing a custom packer tool that randomly tests various packing arrangements until one that’s “good enough” is found. The full story is pretty awesome, and you should definitely give it a read if you haven’t already.
This idea of “randomly trying things until something good-enough is found” appealed to my hacker sensibilities, so I decided to give it a shot.
To work around this incorrect mapping issue, I begin by jittering the
random-seed used by the perfect-hash-function generator, trying to find a set of
hash maps with the least number of incorrect mappings. Once I’ve got something
that seems “good enough” (i.e: whatever minimum I happened to find while
randomly iterating through seeds), I export a static “fixup” table of
uncompressed (shortcode, emoji) pairs, which gets linearly scanned prior to
iterating through the main set of hash tables.
Tada, problem solved! And to think, all we needed to do was spin the wheel a couple times!
This seems to work surprisingly well, with the current dataset only requiring a miniscule ~250 bytes of fixup-table overhead to achieve perfect accuracy for valid inputs (when using a 8-bit key hash).
Note: It turns out that this trick is only useful when using small key hashes that are prone to higher collision rates (such as a simple 8-bit hash). For this particular project, I decided that the slightly larger overhead of using 16-bit hashes outweighed the extra false-positive rates introduced by using an 8-bit hash.
Conclusion⌗
This project has been a real hodgepodge of hacks on top of hacks, but nevertheless, the end result is a lookup function that crunches ~34kb of raw, un-queryable data into a miniscule ~20kb of code + data that can be queried in constant time without requiring any dynamic allocation at runtime. Neato!
Thanks to the power of WebAssembly, you can play with the final result right from your browser!
—-> Check out the online demo! <—–
I’m pretty much done with this project for now, but there are still a few ideas that might be worth exploring to compress things down even more:
- Compressing the emoji UTF-8 strings using some sort of domain specific
representation
- e.g: it seems like most emoji fall under a small subrange of unicode codepoints, it might be possible to shave a couple bits of overhead from each emoji mapping by adding/removing an offset from the stored value.
- Using non-standard key hash sizes (i.e: 9-bit, 10-bit, etc…).
- Follow up: automatically trying out various key hash sizes to minimize space overhead while maintaining a favorable hash-collision rate.
- Actually cleaning up this abomination of a codebase and releasing a proper library that employs these various techniques
Oh, and of course, I should probably port it to one of my keyboards. After all, that was the whole inspiration for this endeavor!
Terrible source code is available on GitHub. The disclaimer at the top of the README file should tell you all you need to know about the quality of the codebase 😬
Acknowledgements⌗
This project wouldn’t have been possible without the incredible
rust-phf library. The in-tree version of
rust-phf is a stripped down version and heavily modified version the library,
optimizing the map’s internal representation for this particular use-case.
The initial POC of this project was based off of https://github.com/kornelski/gh-emoji.
The emoji shortcode database is downloaded directly from GitHub’s gemoji library.
Special thanks to Matt D’Souza and Ethan Hardy, who I nerd-sniped into helping me with this funky little project.